Advertisements
Advertisements
प्रश्न
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.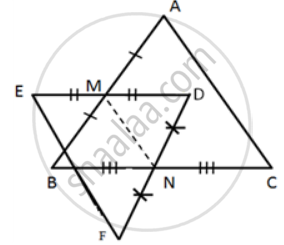
उत्तर
ln ΔEDF,
M is the mid-point of AB and N is the mid-point of DE.
⇒ MN = `1/2`EF ...( Mid-point theorem )
⇒ EF = 2MN ...(i)
ln ΔABC,
M is the mid-point of AB and N is the mid-point of BC,
⇒ MN = `1/2`AC ....( Mid-point theorem )
⇒ AC =2MN ....(ii)
From (i) and (ii), we get
⇒ EF = AC
APPEARS IN
संबंधित प्रश्न
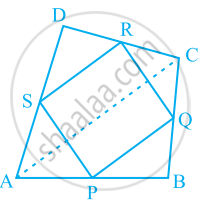
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Fill in the blank to make the following statement correct:
The triangle formed by joining the mid-points of the sides of a right triangle is
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.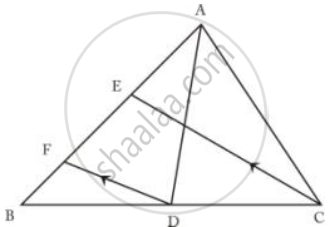
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
