Advertisements
Advertisements
प्रश्न
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

उत्तर
Given: seg PD is a median of ΔPQR. Point T is the mid point of seg PD.
To prove: `"PM"/"PR" = 1/3`
Construction: Draw seg DN || seg QM such that P-M-N and M-N-R.
Proof:
In ΔPDN,
Point T is the mid-point of seg PD. ...(Given)
seg TM || seg DN ...(Construction)
∴ Point M is the mid-point of seg PN. ...(Converse of mid-point theorem)[P-M-N]
∴ PM = MN ...(i)
In ΔQMR,
Point D is the mid-point of seg QR. ...(Given)
seg DN || seg QM. ...(Construction)
∴ Point N is the mid-point of seg MR. ...(Converse of mid-point theorem)[M-N-R]
∴ RN = MN ...(ii)
PM = MN = RN ...[From (i) and (ii)] ...(iii)
Now,
PR = PM + MN + RN
∴ PR = PM + PM + PM ...[From (iii)]
∴ PR = 3PM
∴ `"PM"/"PR" = 1/3`
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
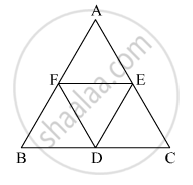
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
