Advertisements
Advertisements
प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
उत्तर

Let ABCD is a quadrilateral in which P,Q, R and S are midpoints of sides
AB, BC,CD and DA respectively join PQ,QR,RS, SP and BD
In ABD, S and P are the midpoints of AD and AB respectively.
So, by using midpoint theorem we can say that
SP || BD and SP = `1/2` BD ......(1)
Similarly in ΔBCD
QR || BD and QR = `1/2` BD .....(2)
From equation (1) and (2) we have
SP || QR and SP = QR
As in quadrilateral SPQR one pair of opposite side are equal and parallel to each other. So, SPQR is parallelogram
Since, diagonals of a parallelogram bisect each other.
Hence PR and QS bisect each other.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.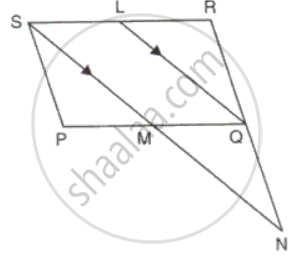
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
