Advertisements
Advertisements
प्रश्न
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if ______.
पर्याय
PQRS is a rhombus
PQRS is a parallelogram
diagonals of PQRS are perpendicular
diagonals of PQRS are equal
उत्तर
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rhombus, if diagonals of PQRS are equal.
Explanation:
Given, the quadrilateral ABCD is a rhombus.
So, sides AB, BC, CD and AD are equal.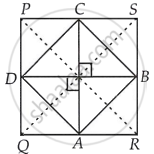
Now, in ΔPQS, we have
D and C are the mid-points of PQ and PS.
So, `DC = 1/2 QS` [By mid-point theorem] ...(i)
Similarly, in ΔPSR, `BC = 1/2 PR` [By mid-point theorem] ...(ii)
As BC = DC ...[Since, ABCD is a rhombus]
∴ `1/2 QS = 1/2 PR` ...[From equations (i) and (ii)]
⇒ QS = PR
Hence, diagonals of PQRS are equal.
APPEARS IN
संबंधित प्रश्न
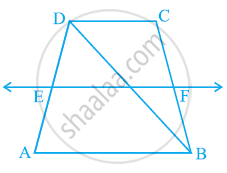
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
Prove that the straight lines joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, ______.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
