Advertisements
Advertisements
प्रश्न
ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see the given figure). Show that F is the mid-point of BC.
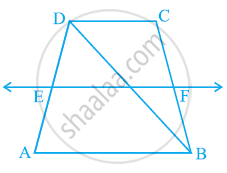
उत्तर
Let EF intersect DB at G.
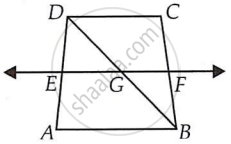
By converse of mid-point theorem, we know that a line drawn through the mid-point of any side of a triangle and parallel to another side, bisects the third side.
In ΔABD,
EF || AB and E is the mid-point of AD.
Therefore, G will be the mid-point of DB.
As EF || AB and AB || CD,
∴ EF || CD ...(Two lines parallel to the same line are parallel to each other)
In ΔBCD, GF || CD and G is the mid-point of line BD. Therefore, by using converse of mid-point theorem, F is the mid-point of BC.
APPEARS IN
संबंधित प्रश्न
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
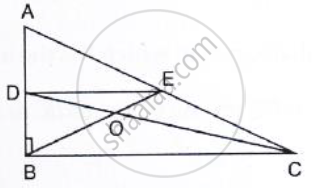
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.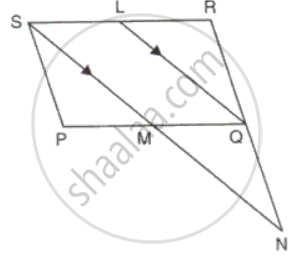
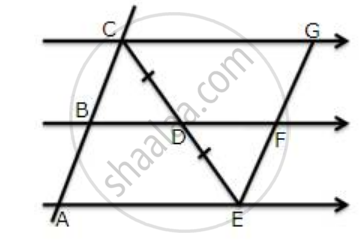
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
The figure obtained by joining the mid-points of the sides of a rhombus, taken in order, is ______.
