Advertisements
Advertisements
प्रश्न
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
पर्याय
PQRS is a rectangle
PQRS is a parallelogram
diagonals of PQRS are perpendicular
diagonals of PQRS are equal
उत्तर
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if diagonals of PQRS are perpendicular.
Explanation:
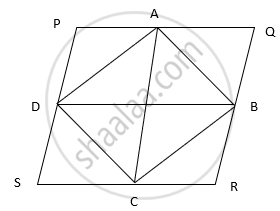
Since, diagonals of rectangle are equal
∴ AC = BD
⇒ PQ = QR
∴ PQRS is a rhombus
Diagonals of a rhombus are perpendicular.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
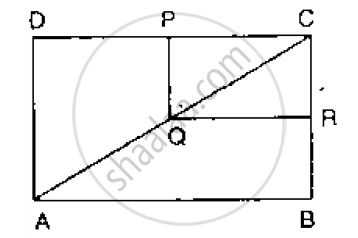
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

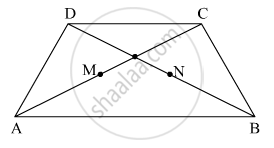
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.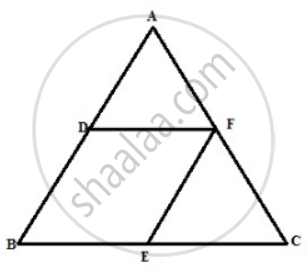
Remark: Figure is incorrect in Question
