Advertisements
Advertisements
प्रश्न
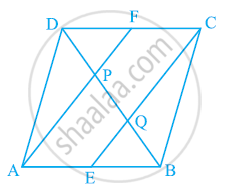
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
उत्तर
ABCD is a parallelogram.
∴ AB || CD
And hence, AE || FC
Again, AB = CD ...(Opposite sides of parallelogram ABCD)
`1/2 AB` = `1/2 CD`
AE = FC ...(E and F are mid-points of side AB and CD)
In quadrilateral AECF, one pair of opposite sides (AE and CF) is parallel and equal to each other. Therefore, AECF is a parallelogram.
⇒ AF || EC ...(Opposite sides of a parallelogram)
In ΔDQC, F is the mid-point of side DC and FP || CQ (as AF || EC). Therefore, by using the converse of mid-point theorem, it can be said that P is the mid-point of DQ.
⇒ DP = PQ ...(1)
Similarly, in ΔAPB, E is the mid-point of side AB and EQ || AP (as AF || EC). Therefore, by using the converse of mid-point theorem, it can be said that Q is the mid-point of PB.
⇒ PQ = QB ...(2)
From equations (1) and (2),
DP = PQ = BQ
Hence, the line segments AF and EC trisect the diagonal BD.
APPEARS IN
संबंधित प्रश्न
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
