Advertisements
Advertisements
प्रश्न
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
उत्तर

Join AC and BC.
In ΔABC, P and Q are the mid-point of AB and BC respectively.
PQ = `(1)/(2)"AC"`.......(i) and PQ || AC
In ΔBDC, R and Q are the mid-points of CD and BC respectively.
QR = `(1)/(2)"BD"`.......(ii) and QR || BD
But AC = BD ...(diagonals of a rectangle)
From (i) and (ii)
PQ = QR
Similarly, QR = RS, RS = SP and RS || AC, SP || BD
Hence, PQ = QR = PS = SP
Therefore, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
In Fig. below, BE ⊥ AC. AD is any line from A to BC intersecting BE in H. P, Q and R are
respectively the mid-points of AH, AB and BC. Prove that ∠PQR = 90°.

Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.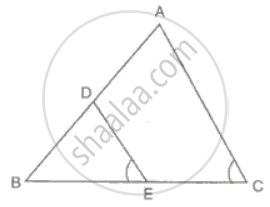
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
E is the mid-point of a median AD of ∆ABC and BE is produced to meet AC at F. Show that AF = `1/3` AC.
