Advertisements
Advertisements
प्रश्न
D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
उत्तर

Given: △ABC, D, E, F are midpoints of AB, BC, AC respectively. AB and DF meet at O. P and Q are midpoints of OB and OC respectively.
To Prove: DPFQ is a parallelogram.
Proof:
In △ABC,
D is the mid-point of AB and F is the mid-point of AC
Hence, DF ∥ BC and DF = `1/2`BC ... (1) (Mid-point theorem)
In △OBC,
P is the mid-point of OB and Q is the mid-point of OC
Hence, PQ ∥ BC and PQ = `1/2`BC ... (2) (mid-point theorem)
thus, from (1) and (2)
DF ∥ PQ and DF = PQ ....(3)
Now, In △AOB,
D is the mid-point of AB and P is the mid-point of OB
Thus, DP ∥ AE and DP = `1/2`AE ....(4) (midpoint theorem)
Now, In △AOC,
F is the midpoint of AC and Q is the midpoint of OC
Thus, FQ ∥ AE and QF = `1/2`AE .....(5) (midpoint theorem)
thus, from (4) and (5)
DP ∥ FQ and DP = FQ .....(6)
DPFQ is a parallelogram ......(from (3) and (6))
Hence proved.
APPEARS IN
संबंधित प्रश्न
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
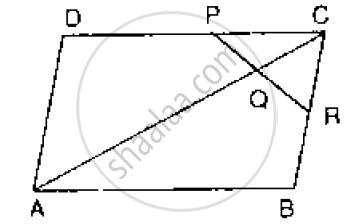
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In a right-angled triangle ABC. ∠ABC = 90° and D is the midpoint of AC. Prove that BD = `(1)/(2)"AC"`.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
