Advertisements
Advertisements
प्रश्न
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
उत्तर
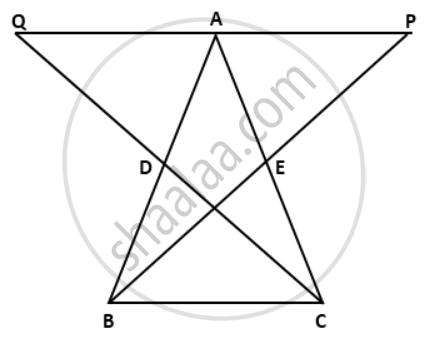
In ΔBDC and ΔADQ,
CD = DQ ....(given)
∠BDC = ∠ADQ ....(vertically opposite angles)
BD = AD ....(D is the mid-point of AB)
∴ ΔBDC ≅ ΔADQ
⇒ ∠DBC = ∠DAQ (c.p.c.t)....(i)
And, BC = AQ (c.p.c.t)....(ii)
Similarly, we can prove ΔCEB ≅ ΔAEP
⇒ ∠ECB = ∠EAP (c.p.c.t)....(iii)
And, BC = AP (c.p.c.t)....(iv)
In ΔABC,
∠ABC + ∠ACB ++ ∠BAC = 180°
⇒ ∠DBC + ∠ECB + ∠BAC = 180°
⇒ ∠DAQ + ∠EAP + ∠BAC = 180° ...[From (i) and (iii)]
⇒ Q, A, P are collinear.
APPEARS IN
संबंधित प्रश्न
Let Abc Be an Isosceles Triangle in Which Ab = Ac. If D, E, F Be the Mid-points of the Sides Bc, Ca and a B Respectively, Show that the Segment Ad and Ef Bisect Each Other at Right Angles.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.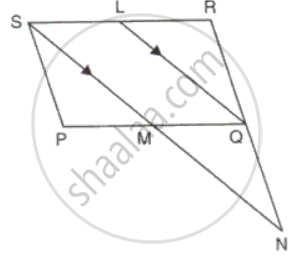
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm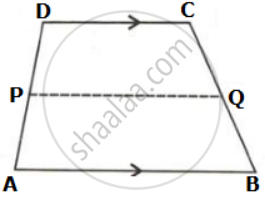
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
