Advertisements
Advertisements
प्रश्न
A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
उत्तर
For help, we draw the diagonal BD as shown below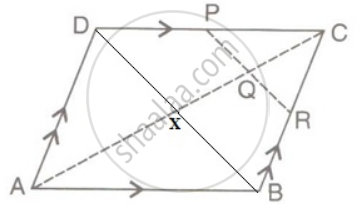
The diagonal AC and BD cuts at point X.
We know that the diagonal of a parallelogram intersect equally with each other. Therefore
AX = CX and BX = DX
Given,
CQ = `[1]/[4]`AC
CQ = `[1]/[4]` x 2CX
CQ = `[1]/[2]`CX
Therefore Q is the midpoint of CX.
(i) For triangle CDX PQ || DX or PR || BD
Since for triangle CBX
Q is the midpoint of CX and QR || BX. Therefore R is the midpoint of BC
(ii) For triangle BCD
As P and R are the mid-point of CD and BC, therefore PR = `[1]/[2]` DB
APPEARS IN
संबंधित प्रश्न
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
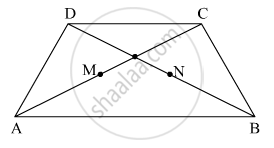
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: ∠EFG = 90°
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
