Advertisements
Advertisements
प्रश्न
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
उत्तर
Given: Let ABCD be a trapezium in which AB || DC and let M and N be the mid-points of the diagonals AC and BD, respectively.
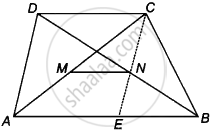
To prove: MN || AB || CD
Construction: Join CN and produce it to meet AB at E.
In ΔCDN and ΔEBN, we have
DN = BN ...[Since, N is the mid-point of BD]
∠DCN = ∠BEN ...[Alternate interior angles]
And ∠CDN = ∠EBN ...[Alternate interior angles]
∴ ΔCDN ≅ ΔEBN ...[By AAS congruence rule]
∴ DC = EB and CN = NE ...[By CPCT rule]
Thus, in ΔCAE, the points M and N are the mid-points of AC and CE, respectively.
∴ MN || AE ...[By mid-point theorem]
⇒ MN || AB || CD
Hence proved.
APPEARS IN
संबंधित प्रश्न
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.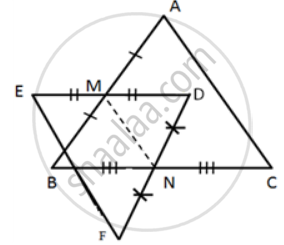
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.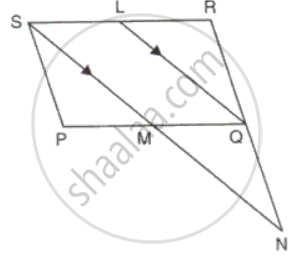
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 4CR = AB.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
