Advertisements
Advertisements
प्रश्न
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
उत्तर
Given: In a quadrilateral ABCD, P, Q, R and S are the mid-points of sides AB, BC, CD and DA, respectively.
Also, AC = BD
To prove: PQRS is a rhombus.
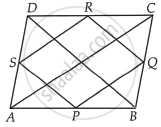
Proof: In ΔADC, S and R are the mid-points of AD and DC respectively.
Then, by mid-point theorem.
SR || AC and SR = `1/2` AC ...(i)
In ΔABC, P and Q are the mid-points of AB and BC respectively.
Then, by mid-point theorem.
PQ || AC and PQ = `1/2` AC ...(ii)
From equations (i) and (ii),
SR = PQ = `1/2` AC ...(iii)
Similarly, in ΔBCD,
RQ || BD and RQ = `1/2` BD ...(iv)
And in ΔBAD,
SP || BD and SP = `1/2` BD ...(v)
From equations (iv) and (v),
SP = RQ = `1/2` BD = `1/2` AC [Given, AC = BD] ...(vi)
From equations (iii) and (vi),
SR = PQ = SP = RQ
It shows that all sides of a quadrilateral PQRS are equal.
Hence, PQRS is a rhombus.
APPEARS IN
संबंधित प्रश्न
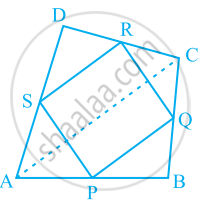
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
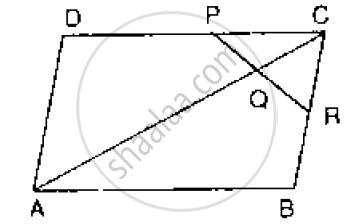
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
In ΔABC, D is the mid-point of AB and E is the mid-point of BC.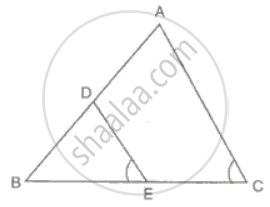
Calculate:
(i) DE, if AC = 8.6 cm
(ii) ∠DEB, if ∠ACB = 72°
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: 2EF = BD.
In ΔABC, D and E are the midpoints of the sides AB and BC respectively. F is any point on the side AC. Also, EF is parallel to AB. Prove that BFED is a parallelogram.
Remark: Figure is incorrect in Question
