Advertisements
Advertisements
प्रश्न
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
उत्तर
Given: E is the mid-point of the side AD of the trapezium ABCD with AB || DC.
Also, EF || AB.
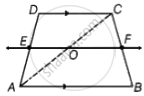
To prove: That F is the mid-point of BC.
Construction: Join AC which intersect EF at O.
Proof: In triangle ADC, E is the mid-point of AD and EF || DC. ...[Since, EF || AB and DC || AB. So, AB || EF || DC]
O is the mid-point of AC and OF || AB.
Now, OF bisect BC. ...[Converse of mid-point theorem]
Or F is the mid-point of BC.
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
Fill in the blank to make the following statement correct
The triangle formed by joining the mid-points of the sides of an isosceles triangle is
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
