Advertisements
Advertisements
प्रश्न
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
उत्तर
The required figure is shown below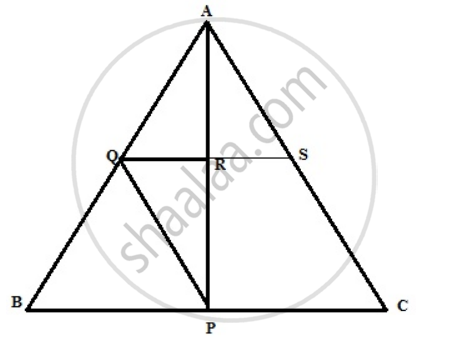
From the figure, it is seen that P is the midpoint of BC and PQ || AC and QR || BC
Therefore Q is the midpoint of AB and R is the midpoint of AP
(i) Therefore AP=2AR
(ii) Here we increase QR so that it cuts AC at S as shown in the figure.
(iii) From triangle PQR and triangle ARS
∠PQR = ∠ARS ...( Opposite angle )
PR = AR
PQ = AS ...[ PQ = AS = `1/2`AC ]
ΔPQR ≅ ΔARS ...( SAS Postulate )
Therefore QR = RS
Now,
BC = 2QS
BC = 2 x 2QR
BC = 4QR
Hence proved.
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
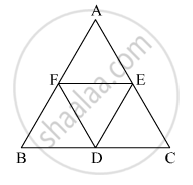
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
