Advertisements
Advertisements
प्रश्न
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
उत्तर
The figure is shown below
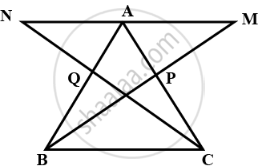
(i) In ΔAQN & ΔBQC
AQ = QB (Given)
∠AQN = ∠BQC
QN = QC
∴ ΔAQN ≅ ΔBQC ...[ by SAS ]
∴ ∠QAN = ∠QBC ...(1)
And BC = AN ……(2)
Similarly, ΔAPM ≅ ΔCPB .....[by SAS]
∠PAM = ∠PCB ...(3) [by CPTC]
And BC = AM ….( 4 )
Now In ΔABC,
∠ABC + ∠ACB + ∠BAC = 180°
∠QAN + ∠PAM + ∠BAC = 180° ...[ (1), (2) we get ]
Therefore M, A, N are collinear.
(ii) From (3) and (4) MA = NA
Hence A is the midpoint of MN.
APPEARS IN
संबंधित प्रश्न
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
