Advertisements
Advertisements
प्रश्न
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
उत्तर
The figure is shown below
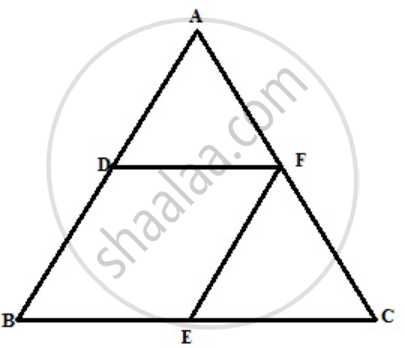
AD = DB BE = EC
EF || AB
In Δ ABC
E is the midpoint of AB and
EF || AB
∴ By the midpoint theorem, F will be the midpoint of AC
As D and F are midpoints of AC and AC respectively
∴ By the midpoint theorem of DF ||BC or BE
Since DF || BE and EF || ED
Hence BEFD is a parallelogram.
APPEARS IN
संबंधित प्रश्न
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
In the given figure, points X, Y, Z are the midpoints of side AB, side BC and side AC of ΔABC respectively. AB = 5 cm, AC = 9 cm and BC = 11 cm. Find the length of XY, YZ, XZ.

L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
