Advertisements
Advertisements
प्रश्न
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
उत्तर
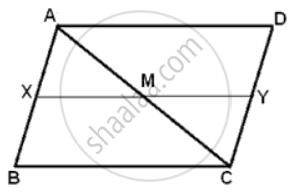
(i) Join XM and MY.
In ΔAXM and ΔCYm
AM = MC ...(given)
AX = CY ...(given)
∠XAM = ∠YCM ...(alternate angles)
Therefore, ΔAXM ≅ ΔCYM.
(ii) ∠AMX + ∠AMY = 180° ...(linear pair of angle = 180°)
THerefore, XMY is a straight line.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.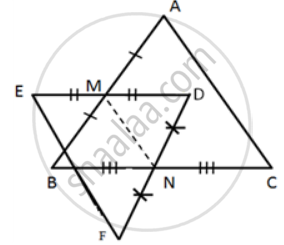
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.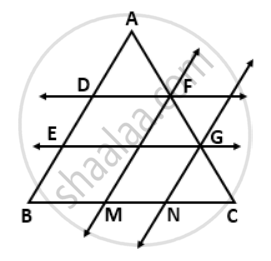
In the given figure, T is the midpoint of QR. Side PR of ΔPQR is extended to S such that R divides PS in the ratio 2:1. TV and WR are drawn parallel to PQ. Prove that T divides SU in the ratio 2:1 and WR = `(1)/(4)"PQ"`.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
