Advertisements
Advertisements
प्रश्न
ABCD is a rhombus, EABF is a straight line such that EA = AB = BF. Prove that ED and FC when produced meet at right angles
उत्तर
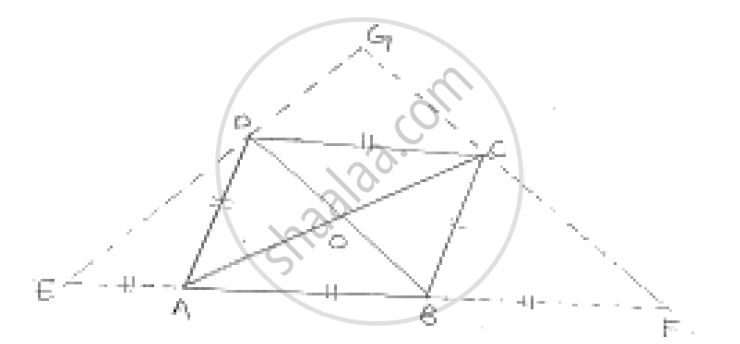
We know that the diagonals of a rhombus are perpendicular bisector of each other
∴ OA = OC, OB = OD, `∠`AOD = `∠`COD = 90°
And `∠`AOB = `∠`COB = 90°
In ΔBDE, A and O are mid points of BE and BD respectively
OA || DE
OC || DG
In ΔCFA, B and O are mid points of AF and AC respectively
∴ OB || CF
OD || GC
Thus, in quadrilateral DOCG, we have
OC || DG and OD || GC
⇒ DOCG is a parallelogram
`∠`DGC = `∠`DOC
`∠`DGC = 90°
APPEARS IN
संबंधित प्रश्न
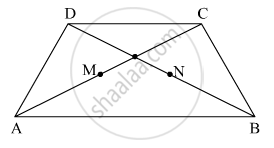
In the adjacent figure, `square`ABCD is a trapezium AB || DC. Points M and N are midpoints of diagonal AC and DB respectively then prove that MN || AB.
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
D, E, and F are the mid-points of the sides AB, BC, and CA respectively of ΔABC. AE meets DF at O. P and Q are the mid-points of OB and OC respectively. Prove that DPQF is a parallelogram.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In ΔABC, X is the mid-point of AB, and Y is the mid-point of AC. BY and CX are produced and meet the straight line through A parallel to BC at P and Q respectively. Prove AP = AQ.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
D and E are the mid-points of the sides AB and AC of ∆ABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is ______.
