Advertisements
Advertisements
प्रश्न
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
उत्तर
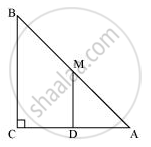
(i) In ΔABC,
It is given that M is the mid-point of AB and MD || BC.
Therefore, D is the mid-point of AC. ...(Converse of mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them, therefore,
∠MDC + ∠DCB = 180° ...(Co-interior angles)
∠MDC + 90° = 180°
∠MDC = 90°
∴ MD ⊥ AC
(iii) Join MC.
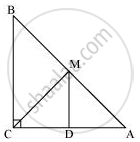
In ΔAMD and ΔCMD,
AD = CD ...(D is the mid-point of side AC)
∠ADM = ∠CDM ...(Each 90º)
DM = DM (Common)
∴ ΔAMD ≅ ΔCMD ...(By SAS congruence rule)
Therefore, AM = CM ...(By CPCT)
However, AM = `1/2AB` ...(M is the mid-point of AB)
Therefore, it can be said that
CM = AM = `1/2AB`
APPEARS IN
संबंधित प्रश्न
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
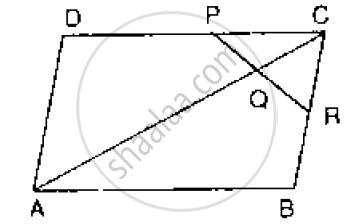
In below Fig, ABCD is a parallelogram in which P is the mid-point of DC and Q is a point on AC such that CQ = `1/4` AC. If PQ produced meets BC at R, prove that R is a mid-point of BC.
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
D and F are midpoints of sides AB and AC of a triangle ABC. A line through F and parallel to AB meets BC at point E.
- Prove that BDFE is a parallelogram
- Find AB, if EF = 4.8 cm.
In triangle ABC, angle B is obtuse. D and E are mid-points of sides AB and BC respectively and F is a point on side AC such that EF is parallel to AB. Show that BEFD is a parallelogram.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: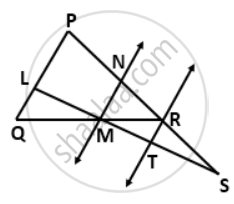
RT = `(1)/(3)"PQ"`
