Advertisements
Advertisements
प्रश्न
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
उत्तर
The figure is as below: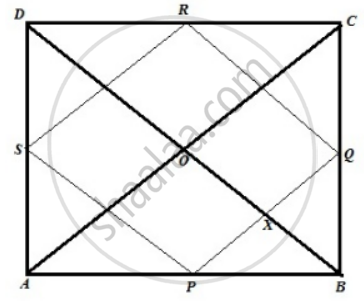
Let ABCD be a quadrilateral where p, Q, R, S are the midpoint of sides AB, BC, CD, DA respectively. Diagonals AC and BD intersect at right angles at point O. We need to show that PQRS is a rectangle
Proof:
In ΔABC and ΔADC,
2PQ = AC and PQ || AC ....(1)
2RS = AC and RS || AC ....(2)
From (1) and (2), we get
PQ = RS and PQ || RS
Similarly, we can show that
PS = RQ and PS || RQ
Therefore, PQRS is a parallelogram.
Now, PQ || AC,
∴ ∠AOD = ∠PXO = 90° ....(Corresponding angles)
Again, BD || RQ,
∴ ∠PXO = ∠RQX = 90° ....(Corresponding angles)
Similarly, ∠QRS = ∠RSP = SPQ = 90°
Therefore, PQRD is a rectangle.
APPEARS IN
संबंधित प्रश्न
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
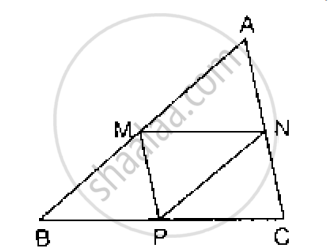
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
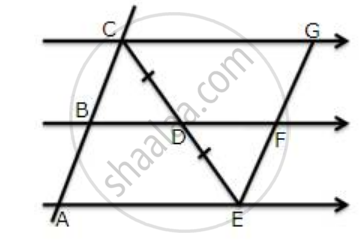
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: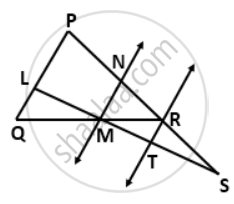
RT = `(1)/(3)"PQ"`
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
