Advertisements
Advertisements
प्रश्न
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
उत्तर
Note: This question is incomplete.
According to the information given in the question,
F could be any point on BC as shown below: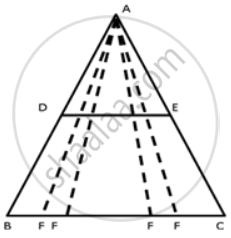
So, this makes it impossible to prove that DP = DE, since P too would shift as F shift because P too would be any point on DE as F is.
Note: If we are given F to be the mid-point of BC, the result can be proved.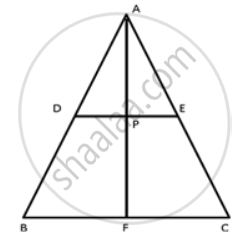
D and E are the mid-points of AB and AC respectively.
DE || BC and DE = `(1)/(2)"BC"`
But F is the mid-point of BC.
⇒ BF = FC = `(1)/(2)"BC"` = DE
Since D is the mid-point of AB, and DP || EF, P is the mid-point of AF.
Since P is the mid-point of AF and E is the mid-point of AC,
PE = `(1)/(2)"FC"`
Also, D and P are the mid-points of AB and AF respectively.
⇒ DP = `(1)/(2)"BF"`
= `(1)/(2)"FC"`
= PE ....(Since BF = FC)
⇒ DP = PE.
APPEARS IN
संबंधित प्रश्न
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
If AE and DF intersect at G, and M and N are the midpoints of GB and GC respectively, prove that DMNF is a parallelogram.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that:
ST = `(1)/(3)"LS"`
D, E and F are respectively the mid-points of the sides AB, BC and CA of a triangle ABC. Prove that by joining these mid-points D, E and F, the triangles ABC is divided into four congruent triangles.
