Advertisements
Advertisements
प्रश्न
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: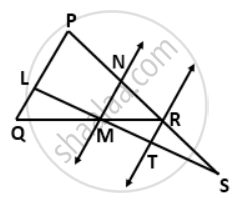
ST = `(1)/(3)"LS"`
उत्तर
Proof :
In ΔPQR,
Since M is the mid-point of QR, and MN || QP, N is the mid-point of PR.
⇒ PN = PR
Given PS = 3RS
⇒ PS = RS = PN + NR + RS
But, PS = PN + NR + Rs
⇒ PN = PR = Rs
⇒R is the mid-point of SN
RT || MN
⇒ T is the mid-point of SM ....(i)
Also, N is the mid-point of PR and MN || LP
⇒ M is the mid-point of LT ....(ii)
So, from (i) and (ii),
LM = MT = ST
⇒ ST = `(1)/(3)"LS"`.
APPEARS IN
संबंधित प्रश्न
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
ABC is a triangle and through A, B, C lines are drawn parallel to BC, CA and AB respectively
intersecting at P, Q and R. Prove that the perimeter of ΔPQR is double the perimeter of
ΔABC
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
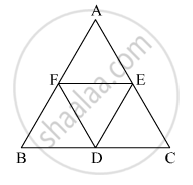
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
In the given figure, AD and CE are medians and DF // CE.
Prove that: FB = `1/4` AB.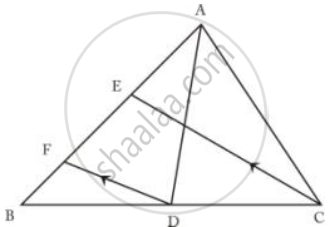
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: AB, if DC = 8 cm and PQ = 9.5 cm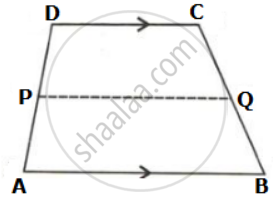
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
