Advertisements
Advertisements
प्रश्न
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: AB, if DC = 8 cm and PQ = 9.5 cm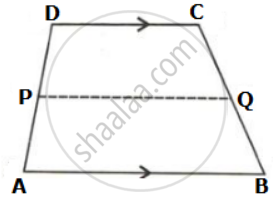
उत्तर
Let us draw a diagonal AC which meets PQ at O as shown below:
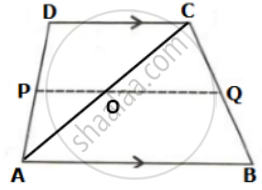
Given DC = 8 cm and PQ = 9.5 cm
In ΔADC,
OP = `(1)/(2)"DC"` ....(Mid-point Theorem)
⇒ OP = `(1)/(2) xx 8` = 4 cm
Now,
OQ = PQ - OP
⇒ OQ = 9.5 - 4
= 5.5 cm
In ΔABC,
OQ = `(1)/(2)"AB"` ....(Mid-point Theorem)
⇒ AB = 2 x OQ
= 2 x 5.5
= 11 cm.
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
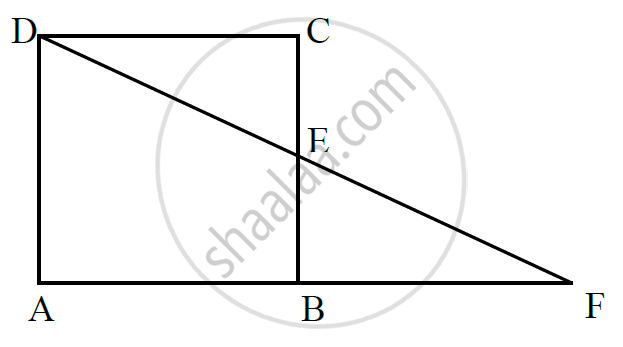
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.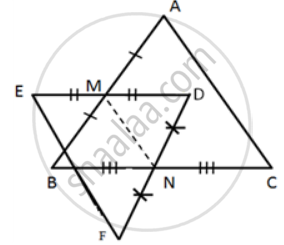
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: A is the mid-point of PQ.
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square is also a square.
E is the mid-point of the side AD of the trapezium ABCD with AB || DC. A line through E drawn parallel to AB intersect BC at F. Show that F is the mid-point of BC. [Hint: Join AC]
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
