Advertisements
Advertisements
प्रश्न
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
उत्तर
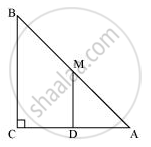
(i) In ΔABC,
It is given that M is the mid-point of AB and MD || BC.
Therefore, D is the mid-point of AC. ...(Converse of mid-point theorem)
(ii) As DM || CB and AC is a transversal line for them, therefore,
∠MDC + ∠DCB = 180° ...(Co-interior angles)
∠MDC + 90° = 180°
∠MDC = 90°
∴ MD ⊥ AC
(iii) Join MC.
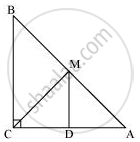
In ΔAMD and ΔCMD,
AD = CD ...(D is the mid-point of side AC)
∠ADM = ∠CDM ...(Each 90º)
DM = DM (Common)
∴ ΔAMD ≅ ΔCMD ...(By SAS congruence rule)
Therefore, AM = CM ...(By CPCT)
However, AM = `1/2AB` ...(M is the mid-point of AB)
Therefore, it can be said that
CM = AM = `1/2AB`
APPEARS IN
संबंधित प्रश्न
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
