Advertisements
Advertisements
प्रश्न
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.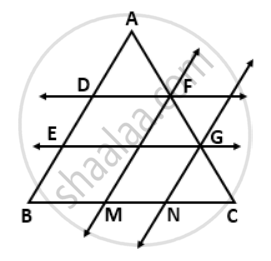
उत्तर

In ΔAEG,
D is the mid-point of AE and DF || EG || BC
Therefore, F is the mid-point of AG.
⇒ AF = FG ....(1)
Again, DF || EG || BC.
Therefore, FG = GC ....(2)
Similarly, since GN || FM || AB,
therefore MB = MN = NC. ...(proved)
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
In a ΔABC, E and F are the mid-points of AC and AB respectively. The altitude AP to BC
intersects FE at Q. Prove that AQ = QP.
ABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP = PH
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

A parallelogram ABCD has P the mid-point of Dc and Q a point of Ac such that
CQ = `[1]/[4]`AC. PQ produced meets BC at R.

Prove that
(i)R is the midpoint of BC
(ii) PR = `[1]/[2]` DB
AD is a median of side BC of ABC. E is the midpoint of AD. BE is joined and produced to meet AC at F. Prove that AF: AC = 1 : 3.
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
