Advertisements
Advertisements
प्रश्न
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
उत्तर
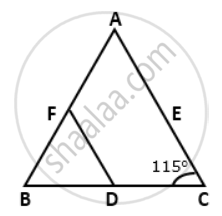
Here, FD || AC
∴ ∠FDB = ∠ACB = 115°. ....(Corresponding angles)
APPEARS IN
संबंधित प्रश्न
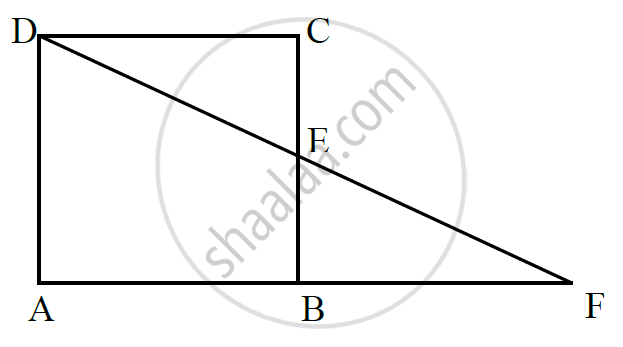
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
In a triangle ∠ABC, ∠A = 50°, ∠B = 60° and ∠C = 70°. Find the measures of the angles of
the triangle formed by joining the mid-points of the sides of this triangle.
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
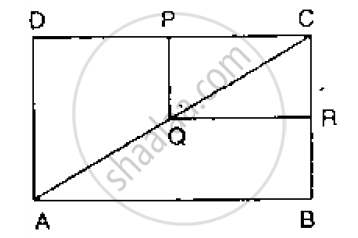
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In a triangle ABC, AD is a median and E is mid-point of median AD. A line through B and E meets AC at point F.
Prove that: AC = 3AF.
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = `1/2` (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
