Advertisements
Advertisements
प्रश्न
E and F are respectively the mid-points of the non-parallel sides AD and BC of a trapezium ABCD. Prove that EF || AB and EF = `1/2` (AB + CD).
[Hint: Join BE and produce it to meet CD produced at G.]
उत्तर
Given: ABCD is a trapezium in which AB || CD. Also, E and F are respectively the mid-points of sides AD and BC.
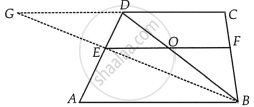
Construction: Join BE and produce it to meet CD produced at G, also draw BD which intersects EF at O.
To prove: EF || AB and EF = `1/2` (AB + CD).
Proof: In ΔGCB, E and F are respectively the mid-points of BG and BC, then by mid-point theorem,
EF || GC
But GC || AB or CD || AB ...[Given]
∴ EF || AB
In ΔADB, AB || EO and E is the mid-point of AD.
Therefore by converse of mid-point theorem, O is mid-point of BD.
Also, EO = `1/2` AB ...(i)
In ΔBDC, OF || CD and O is the mid-point of BD.
∴ OF = `1/2` CD [By converse of mid-point theorem] ...(ii)
On adding equations (i) and (ii), we get
EO + OF = `1/2` AB + `1/2` CD
⇒ EF = `1/2` (AB + CD)
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
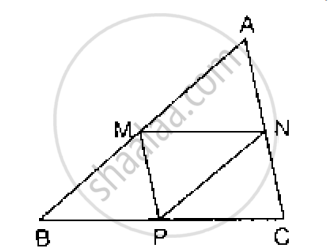
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
In the given figure, `square`PQRS and `square`MNRL are rectangles. If point M is the midpoint of side PR then prove that,
- SL = LR
- LN = `1/2`SQ

In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.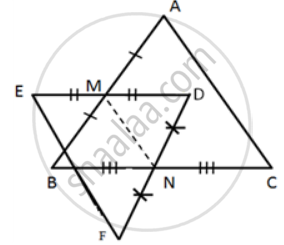
In triangle ABC, AD is the median and DE, drawn parallel to side BA, meets AC at point E.
Show that BE is also a median.
ABCD is a quadrilateral in which AD = BC. E, F, G and H are the mid-points of AB, BD, CD and Ac respectively. Prove that EFGH is a rhombus.

In Δ ABC, AD is the median and DE is parallel to BA, where E is a point in AC. Prove that BE is also a median.
In parallelogram ABCD, E is the mid-point of AB and AP is parallel to EC which meets DC at point O and BC produced at P.
Prove that:
(i) BP = 2AD
(ii) O is the mid-point of AP.
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
