Advertisements
Advertisements
प्रश्न
In `square`ABCD, side BC < side AD in following figure. side BC || side AD and if side BA ≅ side CD then prove that ∠ABC ≅ ∠DCB.

उत्तर

Draw Seg BM ⊥ Seg AD such that A-M-D and Seg CN ⊥ AD so that A-N-D
Seg BC || Seg AD ...(Given)
∴ BM = CN ...(The distance between the lengths of the parallel sides of a parallelogram is equal.) ...(1)
In ∆BMA and ∆CND,
∠BMA = ∠CND = 90°
Hypotenuse BA ≅ Hypotenuse CD ...(Given)
Seg BM ≅ Seg CN ...[From (1)]
∴ ∆BMA ≅ ∆CND ...(Hypotenuse side test)
∴ ∠BAM ≅ ∠CDN ...(c.a.c.t)
That is, ∠BAD ≅ ∠CDA ...(A-M-D, A-N-D) ...(2)
Seg BC || Seg AD ...(Given)
and side AB is their transversal.
∴ ∠ABC + ∠BAD = 180° ...(interior angle) ...(3)
Seg BC || Seg AD ...(Given)
and side CD is their transversal.
∴ ∠DCB + ∠CDA = 180° ...(interior angle) ...(4)
∴ ∠ABC + ∠BAD = ∠DCB + ∠CDA ...[From (3) and (4)]
∴ ∠ABC + ∠CDA = ∠DCB + ∠CDA ...[From (2)]
∴ ∠ABC = ∠DCB
∴ ∠ABC ≅ ∠DCB
APPEARS IN
संबंधित प्रश्न
Explain how this figure is a trapezium. Which of its two sides are parallel?
All parallelograms are trapeziums.
All squares are trapeziums.
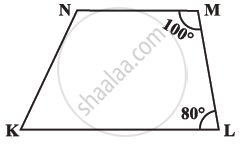
In the given figure CE || DB then the value of x° is
Which of the following properties describe a trapezium?
In trapezium ABCD with AB || CD, if ∠A = 100°, then ∠D = ______.
Every rhombus is a trapezium.
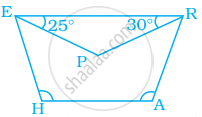
In trapezium HARE, EP and RP are bisectors of ∠E and ∠R respectively. Find ∠HAR and ∠EHA.
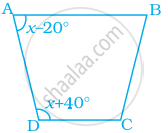
Find the value of x in the trapezium ABCD given below.
Construct a trapezium ABCD in which AB || DC, ∠A = 105°, AD = 3 cm, AB = 4 cm and CD = 8 cm.
