Advertisements
Advertisements
प्रश्न
In `square`ABCD, side BC || side AD, side AB ≅ side DC If ∠A = 72° then find the measure of ∠B and ∠D.
उत्तर

Draw Seg BM ⊥ Seg AD such that A-M-D and Seg CN ⊥ Seg AD so that A-N-D
Seg BC || Seg AD ...(Given)
∴ BM = CN ...(The distance between the lengths of the parallel sides of a parallelogram is equal.)
In ∆BMA and ∆CND,
∠BMA = ∠CND = 90°
Hypotenuse BA ≅ Hypotenuse CD ...(Given)
Seg BM ≅ Seg CN
∴ ∆BMA ≅ ∆CND ...(Hypotenuse side test)
∴ ∠BAM ≅ ∠CDN ...(c.a.c.t)
That is, ∠BAD ≅ ∠CDA ...(A-M-D, A-N-D)
∠BAD = 72° ...(Given)
∠CDA = 72° i.e., ∠D = 72°
Seg BC || Seg AD ...(Given)
side BC || side AD and side BA is their transversal.
∠BAD + ∠ABC = 180° ...(interior angle)
∴ 72° + ∠ABC = 180°
∴ ∠ABC = 180° – 72°
∴ ∠ABC = 108° i.e. ∠B = 108°
APPEARS IN
संबंधित प्रश्न
In `square` IJKL, side IJ || side KL, ∠I = 108°, ∠K = 53° then find the measure of ∠J and ∠L.
In `square`ABCD, side BC < side AD in following figure. side BC || side AD and if side BA ≅ side CD then prove that ∠ABC ≅ ∠DCB.

Which of the following figures satisfy the following property?
- Only one pair of sides are parallel.
All angles of a trapezium are equal.
Every rhombus is a trapezium.
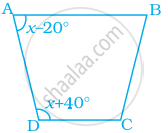
Find the value of x in the trapezium ABCD given below.
In a quadrilateral HOPE, PS and ES are bisectors of ∠P and ∠E respectively. Give reason.
ABCD is a trapezium such that AB || CD, ∠A : ∠D = 2 : 1, ∠B : ∠C = 7 : 5. Find the angles of the trapezium.
Construct a trapezium RISK in which RI || KS, RI = 7 cm, IS = 5 cm, RK = 6.5 cm and ∠I = 60°.
Construct a trapezium ABCD where AB || CD, AD = BC = 3.2 cm, AB = 6.4 cm and CD = 9.6 cm. Measure ∠B and ∠A.
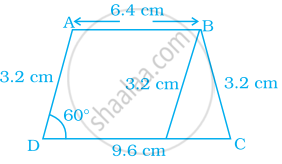
[Hint: Difference of two parallel sides gives an equilateral triangle.]
