Advertisements
Advertisements
Question
In ΔABC, AB = 12 cm and AC = 9 cm. If M is the mid-point of AB and a straight line through M parallel to AC cuts BC in N, what is the length of MN?
Solution

MN || AC and M is mid-point of AB
Therefore, N is mid-point of BC
Hence, MN = `(1)/(2)"AC" = (9)/(2)"cm"` = 4.5cm.
APPEARS IN
RELATED QUESTIONS
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
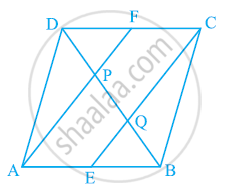
In the below Fig, ABCD and PQRC are rectangles and Q is the mid-point of Prove thaT
i) DP = PC (ii) PR = `1/2` AC
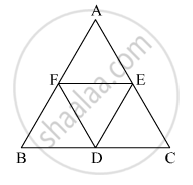
In the given figure, ΔABC is an equilateral traingle. Points F, D and E are midpoints of side AB, side BC, side AC respectively. Show that ΔFED is an equilateral traingle.
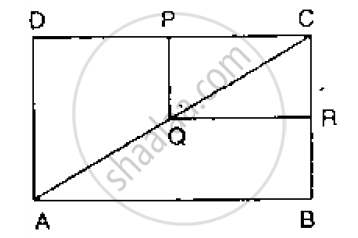
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
D, E, and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC.
Prove that ΔDEF is also isosceles.
In triangle ABC, the medians BP and CQ are produced up to points M and N respectively such that BP = PM and CQ = QN. Prove that:
- M, A, and N are collinear.
- A is the mid-point of MN.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In parallelogram PQRS, L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced at N and cuts side PQ at M. Prove that M is the mid-point of PQ.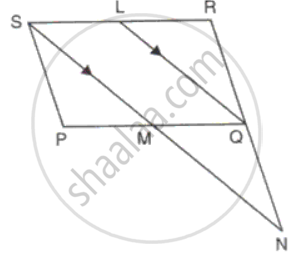
ABCD is a parallelogram.E is the mid-point of CD and P is a point on AC such that PC = `(1)/(4)"AC"`. EP produced meets BC at F. Prove that: F is the mid-point of BC.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD such that AC ⊥ BD. Prove that PQRS is a rectangle.
