Advertisements
Advertisements
Question
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
Solution
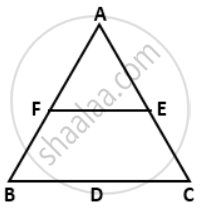
F is the mid-point AB and E is the mid-point of AC.
∴ FE = `(1)/(2)"BC"` ....(Mid-point Theorem)
= `(1)/(2) xx 14`
= 7 cm.
APPEARS IN
RELATED QUESTIONS
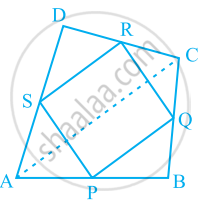
ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA (see the given figure). AC is a diagonal. Show that:
- SR || AC and SR = `1/2AC`
- PQ = SR
- PQRS is a parallelogram.
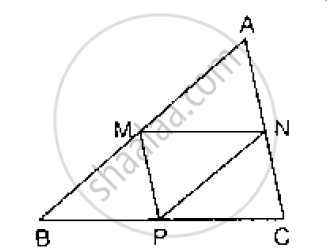
In Fig. below, M, N and P are the mid-points of AB, AC and BC respectively. If MN = 3 cm, NP = 3.5 cm and MP = 2.5 cm, calculate BC, AB and AC.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
In triangle ABC, P is the mid-point of side BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R.
Prove that : (i) AP = 2AR
(ii) BC = 4QR
In triangle ABC ; D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F.
Prove that BDEF is a parallelogram. If AB = 16 cm, AC = 12 cm and BC = 18 cm,
find the perimeter of the parallelogram BDEF.
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
In AABC, D and E are two points on the side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet the side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meet the side BC at points M and N respectively. Prove that BM = MN = NC.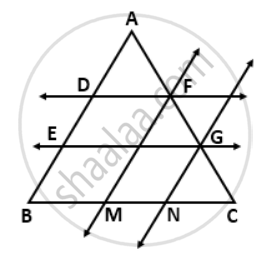
In ∆ABC, AB = 5 cm, BC = 8 cm and CA = 7 cm. If D and E are respectively the mid-points of AB and BC, determine the length of DE.
P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
