Advertisements
Advertisements
Question
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
Solution
The triangle is shown below,

Since M is the midpoint of AB and MN || BC hence N is the midpoint of AC. Therefore
MN = `[1]/ [2]` BC = `[1]/ [2]` x 7 = 3.5cm
And AN = `[1]/ [2]` AC = `[1]/ [2]` x 5 = 2.5cm
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral
bisect each other.
In the given figure, M is mid-point of AB and DE, whereas N is mid-point of BC and DF.
Show that: EF = AC.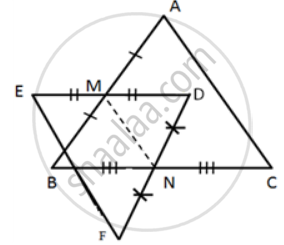
The figure, given below, shows a trapezium ABCD. M and N are the mid-point of the non-parallel sides AD and BC respectively. Find:

- MN, if AB = 11 cm and DC = 8 cm.
- AB, if DC = 20 cm and MN = 27 cm.
- DC, if MN = 15 cm and AB = 23 cm.
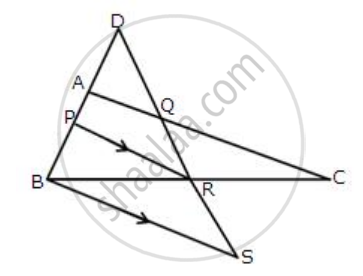
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
