Advertisements
Advertisements
Question
Show that the quadrilateral formed by joining the mid-points of the consecutive sides of a square is also a square.
Solution
Given: In a square ABCD, P, Q, R and S are the mid-points of AB, BC, CD and DA, respectively.
To show: PQRS is a square.
Construction: Join AC and BD.

Proof: Since, ABCD is a square.
∴ AB = BC = CD = AD
Also, P, Q, R and S are the mid-points of AB, BC, CD and DA, respectively.
Then, in ΔADC, SR || AC
And SR = `1/2`AC [By mid-point theorem] ...(i)
In ΔABC, PQ || AC
And PQ = `1/2`AC ...(ii)
From equations (i) and (ii),
SR || PQ and SR = PQ = `1/2`AC ...(iii)
Similarly, SP || BD and BD || RQ
∴ SP || RQ and SP = `1/2`BD
And RQ = `1/2`BD
∴ SP = RQ = `1/2`BD
Since, diagonals of a square bisect each other at right angle.
∴ AC = BD
⇒ SP = RQ = `1/2`AC ...(iv)
From equations (iii) and (iv),
SR = PQ = SP = RQ ...[All side are equal]
Now, in quadrilateral OERF,
OE || FR and OF || ER
∴ ∠EOF = ∠ERF = 90°
Hence, PQRS is a square.
Hence proved.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
In a triangle, P, Q and R are the mid-points of sides BC, CA and AB respectively. If AC =
21 cm, BC = 29 cm and AB = 30 cm, find the perimeter of the quadrilateral ARPQ.
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find ∠FDB if ∠ACB = 115°.
If L and M are the mid-points of AB, and DC respectively of parallelogram ABCD. Prove that segment DL and BM trisect diagonal AC.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: DC, if AB = 20 cm and PQ = 14 cm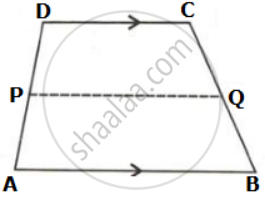
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: Q A and P are collinear.
In ΔABC, the medians BE and CD are produced to the points P and Q respectively such that BE = EP and CD = DQ. Prove that: A is the mid-point of PQ.
