Advertisements
Advertisements
Question
In trapezium ABCD, AB is parallel to DC; P and Q are the mid-points of AD and BC respectively. BP produced meets CD produced at point E.
Prove that:
- Point P bisects BE,
- PQ is parallel to AB.
Solution
The required figure is shown below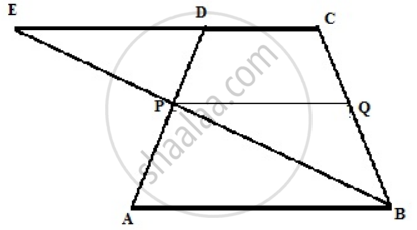
(i) From ΔPED and ΔABP,
PD = AP ...[P is the mid-point of AD]
∠DPE = ∠APB ....[Opposite angle]
∠PED = ∠PBA ...[AB || CE]
∴ ΔPED ≅ ΔABP ...[ASA postulate]
∴ EP = BP
(ii) In Δ ECB,
P is a mid point of BE and
Q is a mid point of BC
∴ PQ || CE ...(i) (by mid point theorem)
and CE || AB ... (ii)
From equation (i) and (ii)
PQ || AB
Hence proved.
APPEARS IN
RELATED QUESTIONS
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
- D is the mid-point of AC
- MD ⊥ AC
- CM = MA = `1/2AB`
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
In triangle ABC, M is mid-point of AB and a straight line through M and parallel to BC cuts AC in N. Find the lengths of AN and MN if Bc = 7 cm and Ac = 5 cm.
In triangle ABC, D and E are points on side AB such that AD = DE = EB. Through D and E, lines are drawn parallel to BC which meet side AC at points F and G respectively. Through F and G, lines are drawn parallel to AB which meets side BC at points M and N respectively. Prove that: BM = MN = NC.
In a parallelogram ABCD, M is the mid-point AC. X and Y are the points on AB and DC respectively such that AX = CY. Prove that:
(i) Triangle AXM is congruent to triangle CYM, and
(ii) XMY is a straight line.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔGEA ≅ ΔGFD
In ΔABC, D and E are the midpoints of the sides AB and AC respectively. F is any point on the side BC. If DE intersects AF at P show that DP = PE.
P and Q are the mid-points of the opposite sides AB and CD of a parallelogram ABCD. AQ intersects DP at S and BQ intersects CP at R. Show that PRQS is a parallelogram.
