Advertisements
Advertisements
Question
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
Solution 1
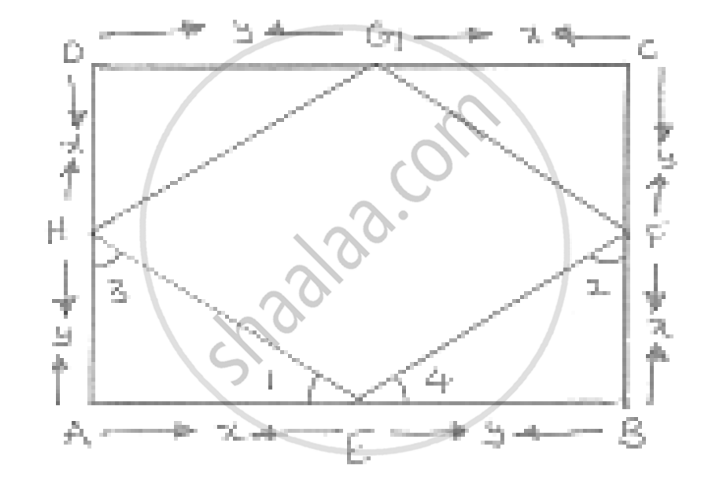
We have
AE = BF = CG = DH = x (say)
∴ BE = CF = DG = AH = y (say)
In Δ ' s AEH and BEF , we have
AE = BF
`∠`A = `∠`B
And AH = BE
So, by SAS configuration criterion, we have
ΔAEH ≅ ΔBFE
⇒ `∠`1 = `∠`2 and `∠`3 = `∠`4
But `∠`1+ `∠`3 = 90° and `∠`2 + `∠`4 = 90°
⇒ `∠`1+ `∠`3+ `∠`2 + `∠`4 = 90° + 90°
⇒ `∠`1+ `∠`4 + `∠`1+ `∠`4 = 180°
⇒ 2 (`∠`1+ `∠`4) = 180°
⇒ `∠`1+ `∠`4 = 90°
HEF = 90°
Similarly we have `∠`F = `∠`G = `∠`H = 90°
Hence, EFGH is a square
Solution 2

We have
AE = BF = CG = DH = x (say)
∴ BE = CF = DG = AH = y (say)
In Δ ' s AEH and BEF , we have
AE = BF
`∠`A = `∠`B
And AH = BE
So, by SAS configuration criterion, we have
ΔAEH ≅ ΔBFE
⇒ `∠`1 = `∠`2 and `∠`3 = `∠`4
But `∠`1+ `∠`3 = 90° and `∠`2 + `∠`4 = 90°
⇒ `∠`1+ `∠`3+ `∠`2 + `∠`4 = 90° + 90°
⇒ `∠`1+ `∠`4 + `∠`1+ `∠`4 = 180°
⇒ 2 (`∠`1+ `∠`4) = 180°
⇒ `∠`1+ `∠`4 = 90°
HEF = 90°
Similarly we have `∠`F = `∠`G = `∠`H = 90°
Hence, EFGH is a square
APPEARS IN
RELATED QUESTIONS
Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
Fill in the blank to make the following statement correct:
The figure formed by joining the mid-points of consecutive sides of a quadrilateral is
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

In trapezium ABCD, sides AB and DC are parallel to each other. E is mid-point of AD and F is mid-point of BC.
Prove that: AB + DC = 2EF.
In ΔABC, BE and CF are medians. P is a point on BE produced such that BE = EP and Q is a point on CF produced such that CF = FQ. Prove that: QAP is a straight line.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
Side AC of a ABC is produced to point E so that CE = `(1)/(2)"AC"`. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meets AC at point P and EF at point R respectively. Prove that: 3DF = EF
In ΔABC, D, E and F are the midpoints of AB, BC and AC.
Show that AE and DF bisect each other.
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: EGFH is a parallelogram.
The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if ______.
