Advertisements
Advertisements
Question
In a parallelogram ABCD, E and F are the midpoints of the sides AB and CD respectively. The line segments AF and BF meet the line segments DE and CE at points G and H respectively Prove that: ΔHEB ≅ ΔHFC
Solution
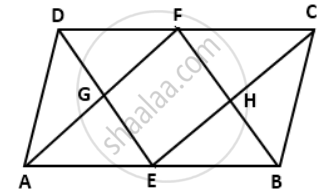
Since ABCD is a parallelogram,
AB = CD and AD = BC
Now, E and F are the mid-points of AB and CD respectively,
⇒ AE = EB = DF = FC ....(i)
In ΔHEB and ΔHFC,
BE = FC ....[From (i)]
∠EHB = ∠FHC ....(vertically opposite angles)
∠HBE = ∠HFC ....(Alternate interior angles)
∴ ΔHEB ≅ ΔHFC.
APPEARS IN
RELATED QUESTIONS
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
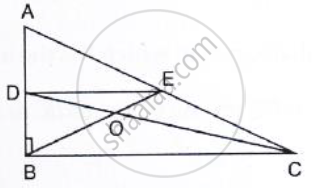
In Fig. below, triangle ABC is right-angled at B. Given that AB = 9 cm, AC = 15 cm and D,
E are the mid-points of the sides AB and AC respectively, calculate
(i) The length of BC (ii) The area of ΔADE.
ABCD is a kite having AB = AD and BC = CD. Prove that the figure formed by joining the
mid-points of the sides, in order, is a rectangle.
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.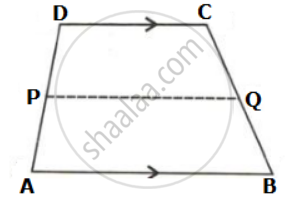
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: AP = 2AR
The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if, ______.
Prove that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of the trapezium.
