Advertisements
Advertisements
Question
The diagonals of a quadrilateral intersect at right angles. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is rectangle.
Solution
The figure is shown below
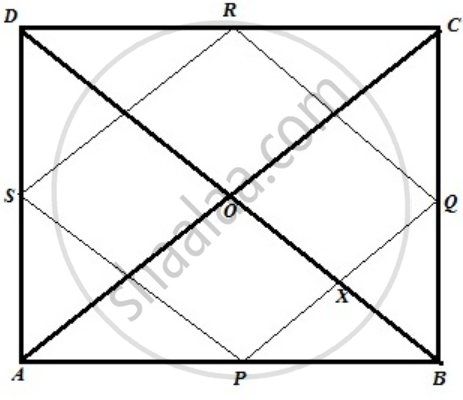
Let ABCD be a quadrilateral where P, Q, R, S are the midpoint of AB, BC, CD, DA. Diagonal AC and BD intersect at a right angle at point O. We need to show that PQRS is a rectangle
Proof:
From and ΔABC and ΔADC
2PQ = AC and PQ || AC …..(1)
2RS = AC and RS || AC …..(2)
From (1) and (2) we get,
PQ = RS and PQ || RS
Similarly, we can show that PS=RQ and PS || RQ
Therefore PQRS is a parallelogram.
Now PQ || AC, therefore ∠AOD = ∠PXO = 90° ...[ Corresponding angel ]
Again BD || RQ, therefore ∠PXO = ∠RQX = 90° ...[ Corresponding angel]
Similarly ∠QRS = ∠RSP = ∠SPQ = 90°
Therefore PQRS is a rectangle.
Hence proved.
APPEARS IN
RELATED QUESTIONS
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
In the given figure, seg PD is a median of ΔPQR. Point T is the mid point of seg PD. Produced QT intersects PR at M. Show that `"PM"/"PR" = 1/3`.
[Hint: DN || QM]

In ∆ABC, E is the mid-point of the median AD, and BE produced meets side AC at point Q.
Show that BE: EQ = 3: 1.
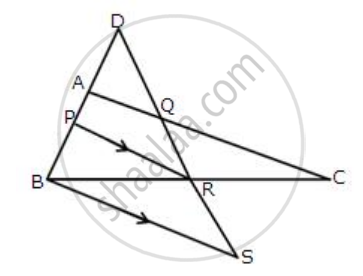
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
If the quadrilateral formed by joining the mid-points of the adjacent sides of quadrilateral ABCD is a rectangle,
show that the diagonals AC and BD intersect at the right angle.
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find DE, if AB = 8 cm
Prove that the figure obtained by joining the mid-points of the adjacent sides of a rectangle is a rhombus.
ABCD is a kite in which BC = CD, AB = AD. E, F and G are the mid-points of CD, BC and AB respectively. Prove that: The line drawn through G and parallel to FE and bisects DA.
In the given figure, PS = 3RS. M is the midpoint of QR. If TR || MN || QP, then prove that: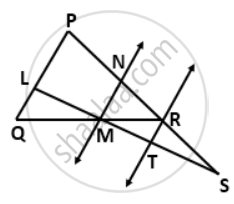
RT = `(1)/(3)"PQ"`
D, E and F are the mid-points of the sides BC, CA and AB, respectively of an equilateral triangle ABC. Show that ∆DEF is also an equilateral triangle.
