Advertisements
Advertisements
Question
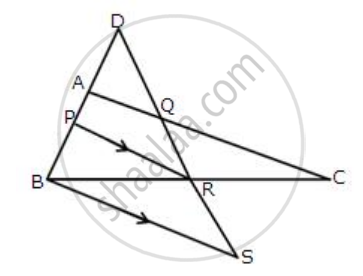
The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
Solution
Consider the figure :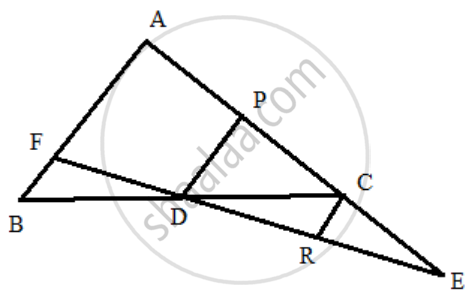
Here D is the midpoint of BC and DP is parallel to AB, therefore P is the midpoint of AC and
PD = `[1]/[2]`AB
(i) Again from the triangle AEF, we have AF || PD || CR and AP = `[1]/[3]`AE
Therefore, DF = `[1]/[3]` EF or we can say that 3DF = EF.
Hence, it is shown.
(ii) From the triangle PED, we have PD || CR and C is the midpoint of PE, therefore, CR = `[1]/[2]`PD
Now,
PD = `1/2` AB
`1/2"PD" = 1/4`AB
CR = `1/4`AB
4CR = AB
Hence, it is shown.
APPEARS IN
RELATED QUESTIONS
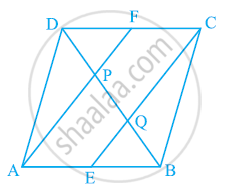
In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively (see the given figure). Show that the line segments AF and EC trisect the diagonal BD.
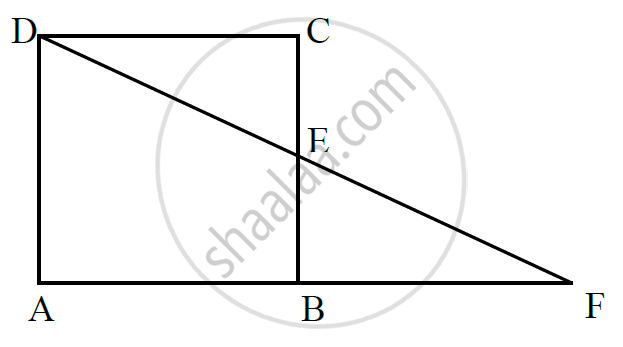
In below fig. ABCD is a parallelogram and E is the mid-point of side B If DE and AB when produced meet at F, prove that AF = 2AB.
In a ∆ABC, D, E and F are, respectively, the mid-points of BC, CA and AB. If the lengths of side AB, BC and CA are 7 cm, 8 cm and 9 cm, respectively, find the perimeter of ∆DEF.
ABC is a triang D is a point on AB such that AD = `1/4` AB and E is a point on AC such that AE = `1/4` AC. Prove that DE = `1/4` BC.
BM and CN are perpendiculars to a line passing through the vertex A of a triangle ABC. If
L is the mid-point of BC, prove that LM = LN.
Use the following figure to find:
(i) BC, if AB = 7.2 cm.
(ii) GE, if FE = 4 cm.
(iii) AE, if BD = 4.1 cm
(iv) DF, if CG = 11 cm.
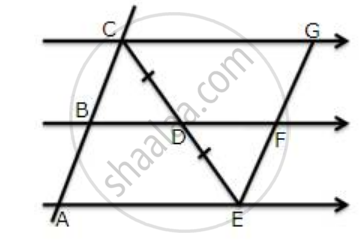
In the figure, give below, 2AD = AB, P is mid-point of AB, Q is mid-point of DR and PR // BS. Prove that:
(i) AQ // BS
(ii) DS = 3 Rs.
In parallelogram ABCD, E and F are mid-points of the sides AB and CD respectively. The line segments AF and BF meet the line segments ED and EC at points G and H respectively.
Prove that:
(i) Triangles HEB and FHC are congruent;
(ii) GEHF is a parallelogram.
In triangle ABC; M is mid-point of AB, N is mid-point of AC and D is any point in base BC. Use the intercept Theorem to show that MN bisects AD.
The diagonals AC and BD of a quadrilateral ABCD intersect at right angles. Prove that the quadrilateral formed by joining the midpoints of quadrilateral ABCD is a rectangle.
