Advertisements
Advertisements
प्रश्न
L and M are the mid-point of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
उत्तर
The required figure is shown below

From figure,
BL = DM and BL || DM and BLMD is a parallelogram, therefore BM || DL
From triangle ABY
L is the midpoint of AB and XL || BY, therefore x is the midpoint of AY.ie AX = XY …..(1)
Similarly for triangle CDX
CY=XY …..(2)
From (1) and (2)
AX = XY = CY and AC = AX + XY + CY
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE = BF = CG = DH. Prove that EFGH is a square.
In a ΔABC, BM and CN are perpendiculars from B and C respectively on any line passing
through A. If L is the mid-point of BC, prove that ML = NL.
The following figure shows a trapezium ABCD in which AB // DC. P is the mid-point of AD and PR // AB. Prove that:
PR = `[1]/[2]` ( AB + CD)

The side AC of a triangle ABC is produced to point E so that CE = AC. D is the mid-point of BC and ED produced meets AB at F. Lines through D and C are drawn parallel to AB which meet AC at point P and EF at point R respectively.
Prove that:
- 3DF = EF
- 4CR = AB
In ΔABC, D, E, F are the midpoints of BC, CA and AB respectively. Find FE, if BC = 14 cm
D, E and F are the mid-points of the sides AB, BC and CA of an isosceles ΔABC in which AB = BC. Prove that ΔDEF is also isosceles.
The diagonals of a quadrilateral intersect each other at right angle. Prove that the figure obtained by joining the mid-points of the adjacent sides of the quadrilateral is a rectangle.
In the given figure, ABCD is a trapezium. P and Q are the midpoints of non-parallel side AD and BC respectively. Find: PQ, if AB = 12 cm and DC = 10 cm.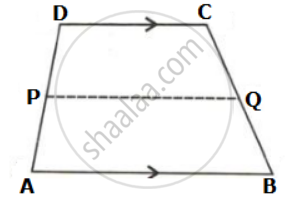
In ΔABC, P is the mid-point of BC. A line through P and parallel to CA meets AB at point Q, and a line through Q and parallel to BC meets median AP at point R. Prove that: BC = 4QR
ΔABC is an isosceles triangle with AB = AC. D, E and F are the mid-points of BC, AB and AC respectively. Prove that the line segment AD is perpendicular to EF and is bisected by it.
