Frank solutions for Mathematics [English] Class 9 ICSE chapter 12 - Isosceles Triangle [Latest edition]

Find the angles of an isosceles triangle whose equal angles and the non - equal angles are in the ratio 3: 4.

Find the angles of an isosceles triangle which are in the ratio 2:2:5.

Each equal angle of an isosceles triangle is less than the third angle by 15°. Find the angles.

Find the interior angles of the following triangles: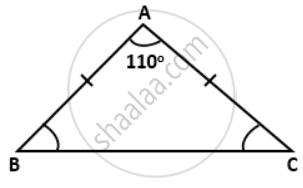

Find the interior angles of the following triangles: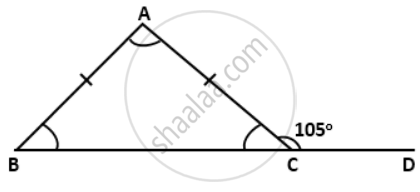

Find the interior angles of the following triangles: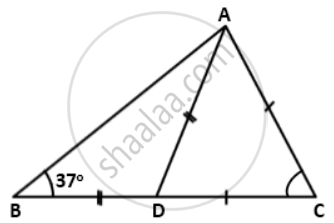

Find the interior angles of the following triangles: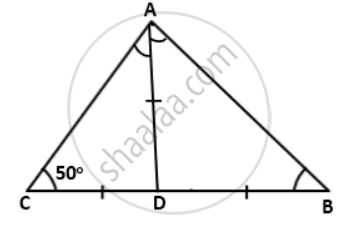

Side BA of an isosceles triangle ABC is produced so that AB = AD. If AB and AC are the equal sides of the isosceles triangle, prove that ∠BCD is a right angle.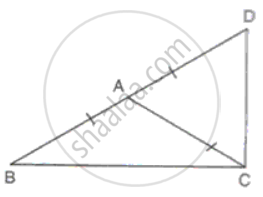

The bisector of the equal angles of an isosceles triangle PQR meet at O. If PQ = PR, prove that PO bisects ∠P.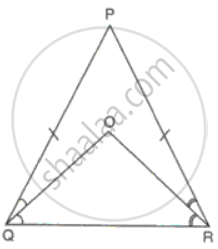

Prove that the medians corresponding to equal sides of an isosceles triangle are equal.

DPQ is an isosceles triangle with DP = DQ. A straight line CD bisects the exterior ∠QDR. Prove that DC is parallel to PQ.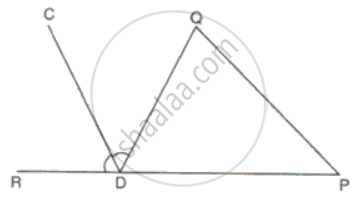

In a quadrilateral PQRS, PQ = PS and RQ = Rs. If ∠50° and ∠R = 110°, find ∠PSR.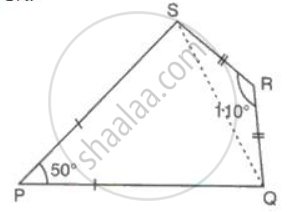

ΔABC is an isosceles triangle with AB = AC. Another triangle BDC is drawn with base BC = BD in such a way that BC bisects ∠B. If the measure of ∠BDC is 70°, find the measures of ∠DBC and ∠BAC.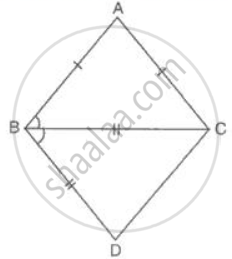

ΔPQR is isosceles with PQ = PR. T is the mid-point of QR, and TM and TN are perpendiculars on PR and PQ respectively. Prove that,
TM = TN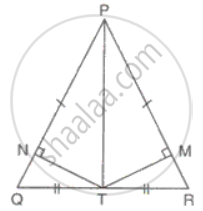

ΔPQR is isosceles with PQ = PR. T is the mid-point of QR, and TM and TN are perpendiculars on PR and PQ respectively. Prove that,
PM = PN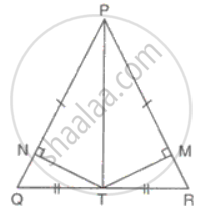 

ΔPQR is isosceles with PQ = PR. T is the mid-point of QR, and TM and TN are perpendiculars on PR and PQ respectively. Prove that,
PT is the bisector of ∠P.

ΔPQR is isosceles with PQ = QR. QR is extended to S so that ΔPRS becomes isosceles with PR = PS. Show that ∠PSRSP : ∠QPS = 1 : 3

In ΔKLM , KT bisects ∠LKM and KT = TM. If ∠LTK is 80°, find the value of ∠LMK and ∠KLM.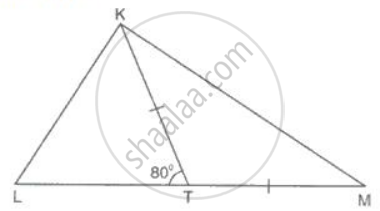

Equal sides QP and RP of an isosceles ΔPQR are produced beyond P to S and T such that ΔPST is an isosceles triangle with PS = PT. Prove that TQ = SR.

Prove that the bisector of the vertex angle of an isosceles triangle bisects the base perpendicularly.

In the figure ΔABC is isosceles with AB = AC. Prove that:
∠A : ∠B = 1 : 3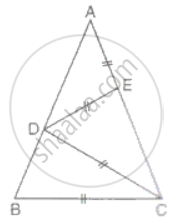

In the figure ΔABC is isosceles with AB = AC. Prove that:
∠ADE = ∠BCD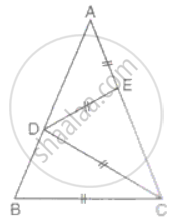

In ΔABC, D is the mid-point of BC, AD is equal to AC. AC is produced to E, such that CE = AC. Prove that:
∠ADB = ∠DCE

In ΔABC, D is the mid-point of BC, AD is equal to AC. AC is produced to E, such that CE = AC. Prove that:
AB = CE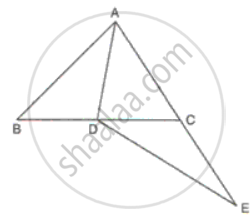

In ΔXYZ, AY and AZ are the bisector of ∠Y and ∠Z respectively. The perpendicular bisectors of AY and AZ cut YZ at B and C respectively. Prove that line segment YZ is equal to the perimeter of ΔABC.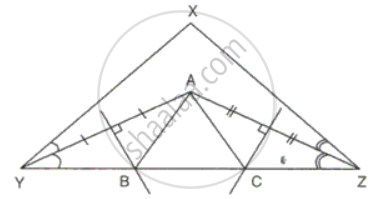

ΔPQR  is an isosceles triangle with PQ = PR. QR is extended to S and ST is drawn perpendicular to QP produced, and SN is perpendicular to PR produced. Prove that QS bisects ∠TSN.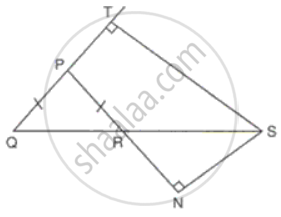

In the given figure, D and E are points on AB and AC respectively. AE and CD intersect at P such that AP = CP. If ∠BAE = ∠BCD, prove that DBDE is isosceles.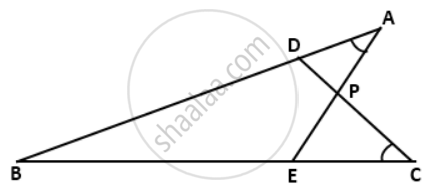

In DPQR as shown, ∠PQS = ∠RQS and QS ⊥ PR. Find the value of x and y, if PQ = 3x + 1; QR = 5y - 2; PS = x + 1 and SR = y + 2.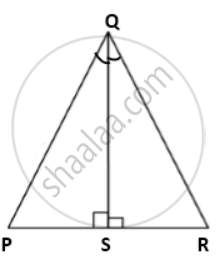

In the given figure :
if ∠PQS = 60°,
find∠QPR.

In the given figure :
if ∠PQS = 60°,
show that PQ = PS = QS = SR.

In the give figure, if DPQR is an isosceles triangle, prove that: ∠QSR = exterior ∠PRT.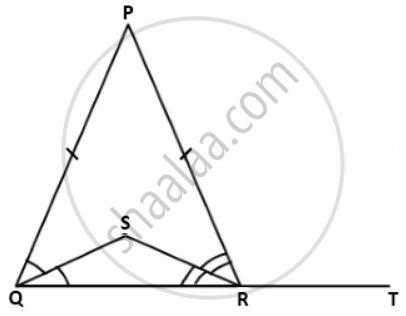

In the given figure, if DABC is an isosceles triangle and ∠PAC = 110^o, find the base angle and vertex angle of the DABC.