Advertisements
Advertisements
प्रश्न
Side BA of an isosceles triangle ABC is produced so that AB = AD. If AB and AC are the equal sides of the isosceles triangle, prove that ∠BCD is a right angle.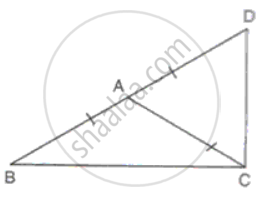
योग
उत्तर
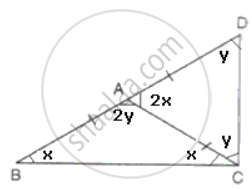
Let ∠ABC = x, therefore ∠BCA = x since AB = AC
In ΔABC,
∠ABC + ∠BCA + ∠BAC = 180° ......(i)
But ∠BAC + ∠DAC = 180° ......(ii)
From (i) and (ii)
∠ABC + ∠BCA + ∠BAC = ∠BAC + ∠DAC
∠DAC = ∠ABC + ∠BCA = x + x = 2x
Let ∠ADC = y, therefore ∠DCA = y since AD = AC
In ΔADC,
∠ADC + ∠DCA + ∠DAC = 180° ......(iii)
But ∠BAc + ∠DAC = 180° ......(iv)
From (iii) and (iv)
∠ADC + ∠DCA + ∠DAC = ∠BAC + ∠DAC
∠BAC = ∠ADC + ∠DCA = y + y = 2y
Substituting the value of ∠BAC and ∠DCA in (ii)
2x + 2y = 180°
x + y = 90°
⇒ ∠BCA + ∠DCA = 90°
⇒ ∠BCD is a right angle.
shaalaa.com
क्या इस प्रश्न या उत्तर में कोई त्रुटि है?
