Advertisements
Chapters
2: Profit , Loss and Discount
3: Compound Interest
4: Expansions
5: Factorisation
6: Changing the subject of a formula
7: Linear Equations
8: Simultaneous Linear Equations
9: Indices
10: Logarithms
11: Triangles and their congruency
12: Isosceles Triangle
13: Inequalities in Triangles
14: Constructions of Triangles
15: Mid-point and Intercept Theorems
16: Similarity
17: Pythagoras Theorem
18: Rectilinear Figures
19: Quadrilaterals
20: Constructions of Quadrilaterals
▶ 21: Areas Theorems on Parallelograms
22: Statistics
23: Graphical Representation of Statistical Data
24: Perimeter and Area
25: Surface Areas and Volume of Solids
26: Trigonometrical Ratios
27: Trigonometrical Ratios of Standard Angles
28: Coordinate Geometry
![Frank solutions for Mathematics [English] Class 9 ICSE chapter 21 - Areas Theorems on Parallelograms Frank solutions for Mathematics [English] Class 9 ICSE chapter 21 - Areas Theorems on Parallelograms - Shaalaa.com](/images/mathematics-english-class-9-icse_6:c41cc344f5174c64a036c55d113af73f.jpg)
Advertisements
Solutions for Chapter 21: Areas Theorems on Parallelograms
Below listed, you can find solutions for Chapter 21 of CISCE Frank for Mathematics [English] Class 9 ICSE.
Frank solutions for Mathematics [English] Class 9 ICSE 21 Areas Theorems on Parallelograms Exercise 21.1 [Pages null - 25]
ABCD is a parallelogram having an area of 60cm2. P is a point on CD. Calculate the area of ΔAPB.
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
In the figure, PT is parallel to SR. QTSR is a parallelogram and PQSR is a rectangle. If the area of ΔQTS is 60cm2, find:
(i) the area o || gm QTSR
(ii) the area of the rectangle PQRS
(iii) the area of the triangle PQS.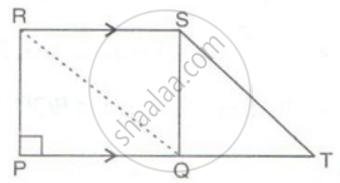
In the given figure area of ∥ gm PQRS is 30 cm2. Find the height of ∥ gm PQFE if PQ = 6 cm.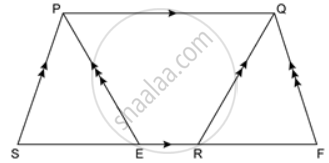
In the given figure, PQRS is a ∥ gm. A straight line through P cuts SR at point T and QR produced at N. Prove that area of triangle QTR is equal to the area of triangle STN.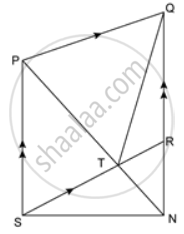
In the given figure, ST ∥ PR. Prove that: area of quadrilateral PQRS = area of ΔPQT.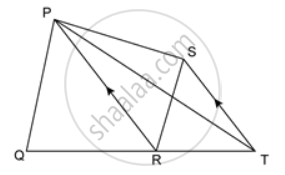
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.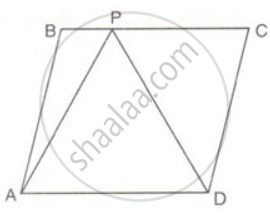
In the figure, if the area of ||gm PQRS is 84cm2; find the area of
(i) || gm PQMN
(ii) ΔPQS
(iii) ΔPQN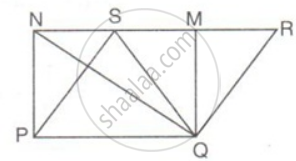
In the figure, PQR is a straight line. SQ is parallel to Tp. Prove that the quadrilateral PQST is equal in area to the ΔPSR.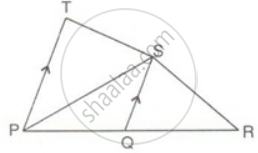
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.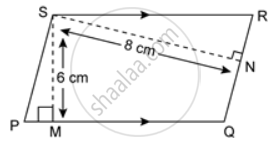
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.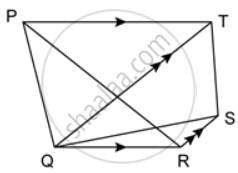
*Question modified
In the given figure, ΔPQR is right-angled at P. PABQ and QRST are squares on the side PQ and hypotenuse QR. If PN ⊥ TS, show that:
(a) ΔQRB ≅ ΔPQT
(b) Area of square PABQ = area of rectangle QTNM.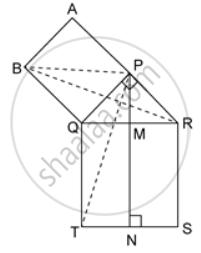
In the figure, AE = BE. Prove that the area of triangle ACE is equal in area to the parallelogram ABCD.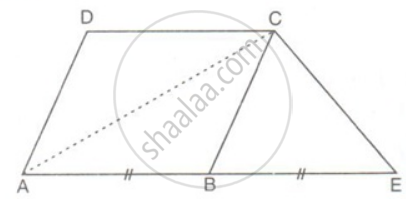
The diagonals of a parallelogram ABCD intersect at O. A line through O meets AB in P and CD in Q. Show that
(a) Area of APQD = `(1)/(2)` area of || gm ABCD
(b) Area of APQD = Area of BPQC
Prove that the median of a triangle divides it into two triangles of equal area.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
In the given figure AF = BF and DCBF is a parallelogram. If the area of ΔABC is 30 square units, find the area of the parallelogram DCBF.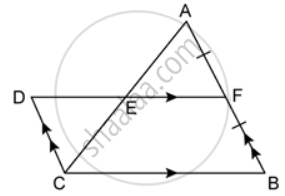
Prove that the diagonals of a parallelogram divide it into four triangles of equal area.
The diagonals AC and BC of a quadrilateral ABCD intersect at O. Prove that if BO = OD, then areas of ΔABC an ΔADC area equal.
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
PQRS is a parallelogram and O is any point in its interior. Prove that: area(ΔPOQ) + area(ΔROS) - area(ΔQOR) + area(ΔSOP) = `(1)/(2)`area(|| gm PQRS)
A quadrilateral ABCD is such that diagonals BD divides its area into two equal parts. Prove that BD bisects AC.
In the given figure, BC ∥ DE.
(a) If area of ΔADC is 20 sq. units, find the area of ΔAEB.
(b) If the area of ΔBFD is 8 square units, find the area of ΔCEF
ΔPQR and ΔSQR are on the same base QR with P and S on opposite sides of line QR, such that area of ΔPQR is equal to the area of ΔSQR. Show that QR bisects PS.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
In ΔABC, the mid-points of AB, BC and AC are P, Q and R respectively. Prove that BQRP is a parallelogram and that its area is half of ΔABC.
In the given figure, PQ ∥ SR ∥ MN, PS ∥ QM and SM ∥ PN. Prove that: ar. (SMNT) = ar. (PQRS).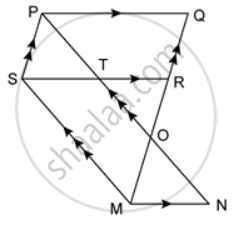
In ΔPQR, PS is a median. T is the mid-point of SR and M is the mid-point of PT. Prove that: ΔPMR = `(1)/(8)Δ"PQR"`.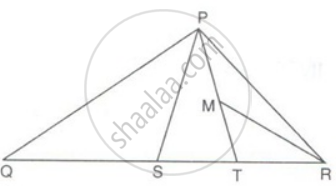
In the figure, ABCD is a parallelogram and CP is parallel to DB. Prove that: Area of OBPC = `(3)/(4)"area of ABCD"`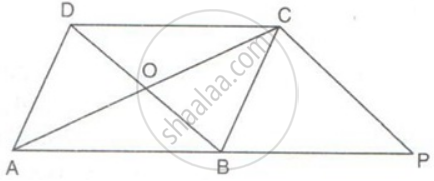
The medians QM and RN of ΔPQR intersect at O. Prove that: area of ΔROQ = area of quadrilateral PMON.
In the given figure, ABC is a triangle and AD is the median.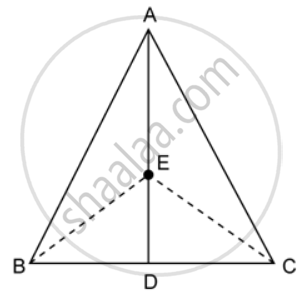
If E is any point on the median AD. Show that: Area of ΔABE = Area of ΔACE.
In the given figure, ABC is a triangle and AD is the median.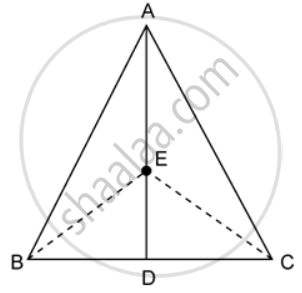
If E is the midpoint of the median AD, prove that: Area of ΔABC = 4 × Area of ΔABE
In a parallelogram PQRS, M and N are the midpoints of the sides PQ and PS respectively. If area of ΔPMN is 20 square units, find the area of the parallelogram PQRS.
In a parallelogram PQRS, T is any point on the diagonal PR. If the area of ΔPTQ is 18 square units find the area of ΔPTS.
ABCD is a quadrilateral in which diagonals AC and BD intersect at a point O. Prove that: areaΔAOD + areaΔBOC + areaΔABO + areaΔCDO.
In the given figure, AB ∥ SQ ∥ DC and AD ∥ PR ∥ BC. If the area of quadrilateral ABCD is 24 square units, find the area of quadrilateral PQRS.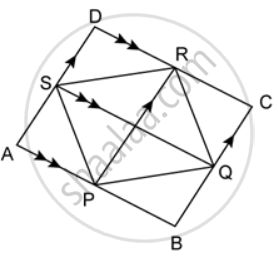
Solutions for 21: Areas Theorems on Parallelograms
![Frank solutions for Mathematics [English] Class 9 ICSE chapter 21 - Areas Theorems on Parallelograms Frank solutions for Mathematics [English] Class 9 ICSE chapter 21 - Areas Theorems on Parallelograms - Shaalaa.com](/images/mathematics-english-class-9-icse_6:c41cc344f5174c64a036c55d113af73f.jpg)
Frank solutions for Mathematics [English] Class 9 ICSE chapter 21 - Areas Theorems on Parallelograms
Shaalaa.com has the CISCE Mathematics Mathematics [English] Class 9 ICSE CISCE solutions in a manner that help students grasp basic concepts better and faster. The detailed, step-by-step solutions will help you understand the concepts better and clarify any confusion. Frank solutions for Mathematics Mathematics [English] Class 9 ICSE CISCE 21 (Areas Theorems on Parallelograms) include all questions with answers and detailed explanations. This will clear students' doubts about questions and improve their application skills while preparing for board exams.
Further, we at Shaalaa.com provide such solutions so students can prepare for written exams. Frank textbook solutions can be a core help for self-study and provide excellent self-help guidance for students.
Concepts covered in Mathematics [English] Class 9 ICSE chapter 21 Areas Theorems on Parallelograms are Introduction of Rectilinear Figures, Names of Polygons, Concept of Quadrilaterals, Diagonal Properties of Different Kinds of Parallelograms, Property: The Diagonals of a Rectangle Are of Equal Length., Property: The diagonals of a square are perpendicular bisectors of each other., Types of Quadrilaterals, Property: The Opposite Sides of a Parallelogram Are of Equal Length., Property: The Opposite Angles of a Parallelogram Are of Equal Measure., Property: The diagonals of a rhombus are perpendicular bisectors of one another..
Using Frank Mathematics [English] Class 9 ICSE solutions Areas Theorems on Parallelograms exercise by students is an easy way to prepare for the exams, as they involve solutions arranged chapter-wise and also page-wise. The questions involved in Frank Solutions are essential questions that can be asked in the final exam. Maximum CISCE Mathematics [English] Class 9 ICSE students prefer Frank Textbook Solutions to score more in exams.
Get the free view of Chapter 21, Areas Theorems on Parallelograms Mathematics [English] Class 9 ICSE additional questions for Mathematics Mathematics [English] Class 9 ICSE CISCE, and you can use Shaalaa.com to keep it handy for your exam preparation.
