Advertisements
Advertisements
प्रश्न
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.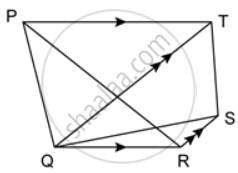
*Question modified
उत्तर
Joining TR, we get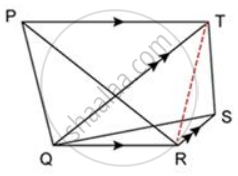
ΔPQR and ΔQTR are on the same base QR and between the same parallel lines QR and PT.
∴ A(ΔPQR) = A(ΔQTR) ....(i)
ΔQTR and ΔTQS are on the same base QT and between the same parallel lines QT and RS.
∴ A(ΔQRT) = A(ΔTQS) ....(ii)
From (i) and (ii), we get
A(ΔPQR) = A(ΔTQS).
APPEARS IN
संबंधित प्रश्न
Diagonal AC of a parallelogram ABCD bisects ∠A (see the given figure). Show that
- It bisects ∠C also,
- ABCD is a rhombus

In parallelogram ABCD, AP and AQ are perpendiculars from the vertex of obtuse angle A as shown.
If ∠x: ∠y = 2: 1.
find angles of the parallelogram.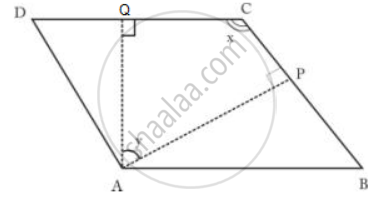
State, 'true' or 'false'
The diagonals of a quadrilateral bisect each other.
State, 'true' or 'false'
Each diagonal of a rhombus bisects it.
State, 'true' or 'false'
Every rhombus is a parallelogram.
State, 'true' or 'false'
Every parallelogram is a rhombus.
In the following figures, ABCD is a parallelogram.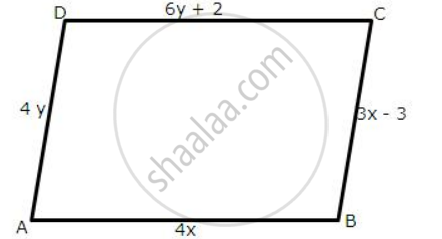
find the values of x and y.
In the following figures, ABCD is a parallelogram.

Find the values of x and y.
In the given figure ABCD is a rhombus with angle A = 67°

If DEC is an equilateral triangle, calculate:
- ∠CBE
- ∠DBE
PQRS is a rectangle in which PQ = 12cm and PS = 8cm. Calculate the area of ΔPRS.
If the medians of a ΔABBC intersect at G, show that ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) = `(1)/(3)"ar(ΔABC)"`.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
The length and breadth of a rectangular field are in the ratio 8 : 5. A 2m wide path runs all around outside the field. The area of the path is 848m2. Find the length and breadth of the field.
The perimeter of a rectangular plot is 300m. It has an area of 5600m2. Taking the length of the plot as x m, calculate the breadth of the plot in terms of x, form an equation and solve it to find the dimensions of the plot.
Each angle of a rectangle is a right angle.
Give reasons for the following :
A rectangle can be thought of as a special parallelogram.
Give reason for the following :
Squares, rectangles, parallelograms are all quadrilaterals.
