Advertisements
Advertisements
प्रश्न
In the given figure, PT ∥ QR and QT ∥ RS. Show that: area of ΔPQR = area of ΔTQS.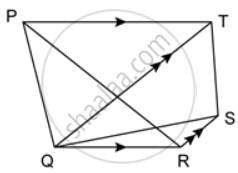
*Question modified
उत्तर
Joining TR, we get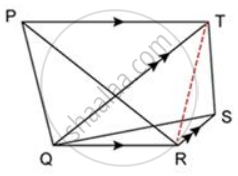
ΔPQR and ΔQTR are on the same base QR and between the same parallel lines QR and PT.
∴ A(ΔPQR) = A(ΔQTR) ....(i)
ΔQTR and ΔTQS are on the same base QT and between the same parallel lines QT and RS.
∴ A(ΔQRT) = A(ΔTQS) ....(ii)
From (i) and (ii), we get
A(ΔPQR) = A(ΔTQS).
APPEARS IN
संबंधित प्रश्न
State, 'true' or 'false'
Every rhombus is a parallelogram.
In the figure, ABCD is a parallelogram and APD is an equilateral triangle of side 80cm, Calculate the area of parallelogram ABCD.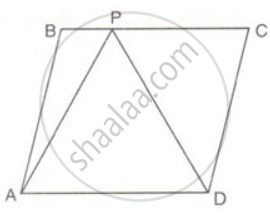
In the given figure, if AB ∥ DC ∥ FG and AE is a straight line. Also, AD ∥ FC. Prove that: area of ∥ gm ABCD = area of ∥ gm BFGE.
AD is a median of a ΔABC.P is any point on AD. Show that the area of ΔABP is equal to the area of ΔACP.
Find the area of a parallelogram whose base is 12cm and the height is 5cm.
One side of a parallelogram is 12cm and the altitude corresponding to i is 8cm. If the length of the altitude corresponding to its adjacent side is 16cm, find the length of the adjacent side.
Two adjacent sides of a parallelogram are 20cm and 18cm. If the distance between the larger sides is 9cm, find the area of the parallelogram. Also, find the distance between the shorter sides.
The area of a square garden is equal to the area of a rectangular plot of length 160m and width 40m. Calculate the cost of fencing the square garden at Rs.12per m.
Find the area of a square whose diagonal is `12sqrt(12)"cm"`
The area of a square plot of side 80m is equal to the area of a rectangular plot of length 160m. Calculate the width of the rectangular plot and the cost of fencing it Rs.7.50per m.
The side of a square exceeds the side of another square by 4cm and the sum of the areas of the squares is 400cm2. Find the dimensions of the squares.
Find the area of a rhombus, whose one side and one diagonal measure 20cm and 24cm respectively.
The area of a rhombus is 234 cm2. If its one diagonal is 18 cm, find the lengths of its side and the other diagonal. Also, find perimeter of the rhombus.
PQRS is a square with each side 6cm. T is a point on QR such that the `"area of ΔPQT"/"area of trapezium PTRS" = (1)/(3)` Find the length of TR.
The opposite sides of a trapezium are parallel.
A figure is said to be regular if its sides are equal in length and angles are equal in measure. Can you identify the regular quadrilateral?
Examine whether the following is a polygon. If it is not, say why?

Name polygon.

Make two more examples of this.
