Advertisements
Advertisements
प्रश्न
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.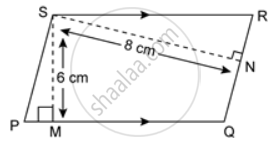
उत्तर
Area of ||gm PQRS = PQ x 6
Also,
Area of ||gm PQRS = PS x 8
∴ PQ x 6 = PS x 8
⇒ PQ = `(8"PS")/(6)`
⇒ PQ = `(4"PS")/(3)` ....(i)
Perimeter of ||gm PQRS = PQ + OR + RS + PS
⇒ 42 = 2PQ + 2PS ...(opposite sides of a parallelogram are equal)
⇒ 21 = PQ + PS
⇒ `(4"PS")/(3) + "PS"` = 21 ...[From (i)]
⇒ `(4"PS" + 3"PS")/(3)`
⇒ 7PS = 63
⇒ PS = 9cm
Now,
PQ = `(4"PS")/(3)`
= `(4 xx 9)/(3)`
= 12cm
∴ PQ = 12cm and PS = 9cm.
APPEARS IN
संबंधित प्रश्न
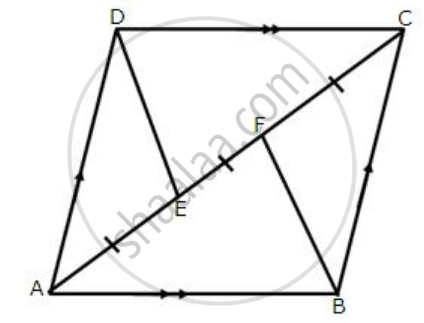
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2 AD.
Prove that:
(i) BP bisects angle B.
(ii) Angle APB = 90o.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.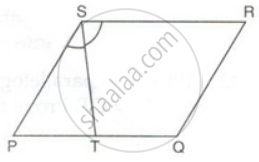
Prove that: RT bisects angle R
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.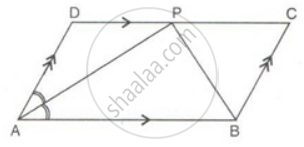
Prove that: ∠APB is a right angle.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.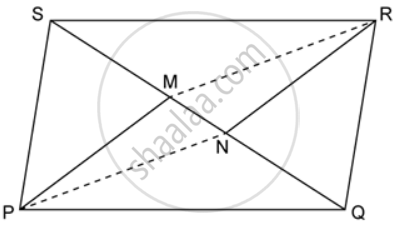
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
Find the perimeter of the parallelogram PQRS.

In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
