Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.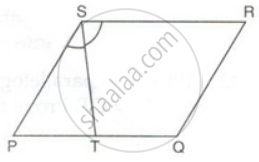
Prove that: RT bisects angle R
उत्तर

Since QT = QR
∠QTR = ∠QRT
But ∠QTR = ∠TRS ...(alternate angles ∵ SR || PQ)
⇒ ∠QRT = ∠TRS
Therefore, RT bisects ∠R.
APPEARS IN
संबंधित प्रश्न
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 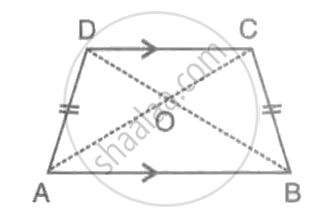
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
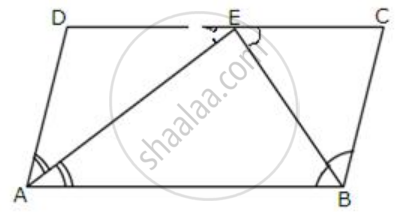
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
Find the perimeter of the parallelogram PQRS.

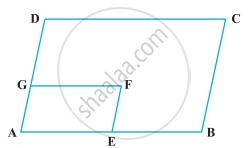
In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.