Advertisements
Advertisements
प्रश्न
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
उत्तर
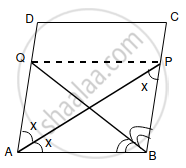
Given: ABCD is a parallelogram and AP bisects ∠A and BQ bisects ∠B.
To prove:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
Proofs:
Let ∠QAB = 2x
∠ABP = 180 - 2x
∠PAB = x
∠APB = 180 - (x + 180 - 2x)
= 180 - (180 - x)
= 180 - 180 + x
= x
In ΔBAP,
∠BAP = ∠APB
or AB = BP ...(1)
Now, ∠PBA = 180 - 2x
∠PBQ = ∠QBA
∠QBA = `(180 - 2x)/2`
= 90 - x
So, ∠PBQ = 90 - x
and ∠PBQ = ∠AQB ...[Alternate Interior Angles]
∠AQB = 90 - x
∠QBA = ∠AQB
hence, AB = AQ ...(2)
From equations (1) & (2) we get
∴ AQ = PB
Since, AQ = BP & ...(As ABCD is Parallelogram)
AQ || PB ...(Opposite sides are equal & parallel, So, ABPQ is a parallelogram)
AB = PQ ...(As ABPQ is a parallelogram)
and AB = CD ...(As ABCD is a parallelogram)
Hence, CD = PQ
APPEARS IN
संबंधित प्रश्न
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
Prove that the bisectors of opposite angles of a parallelogram are parallel.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 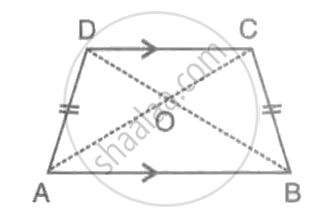
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.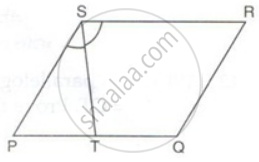
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.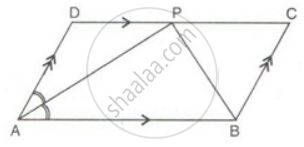
Prove that: BP bisects ∠ABC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.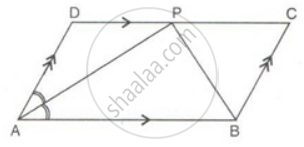
Prove that: ∠APB is a right angle.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD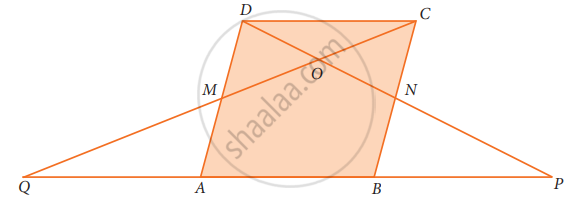
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?