Advertisements
Advertisements
प्रश्न
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 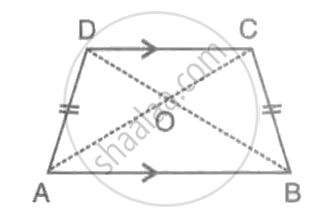
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
उत्तर
Given ABCD is a trapezium, AB || DC and AD = BC.
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
Proof: (i) Since AD || CB and transversal AC cuts them at A and O respectively.
Therefore, ∠A + ∠B = 180°
Since, AB || CD and AD || BC
Therefore, ABCD is a parallelogram.
∠A = ∠C
∠B = ∠D ....[ Since ABCD is a parallelogram ]
Therefore,
∠DAB = ∠CBA
∠ADC = ∠BCD
In ΔABC and ΔBAD, we have
BC = AD ....( given )
AB = BA ....( Common )
∠A = ∠B ....( proved )
ΔABC ≅ ΔBAD ....( SAS )
ΔABC ≅ ΔBAD
Since, Therefore AC = BD....( Corresponding parts of congruent triangles are equal. )
OA = OB
Again OC = OD ....( Since diagonals bisect each other at O )
Hence proved.
APPEARS IN
संबंधित प्रश्न
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
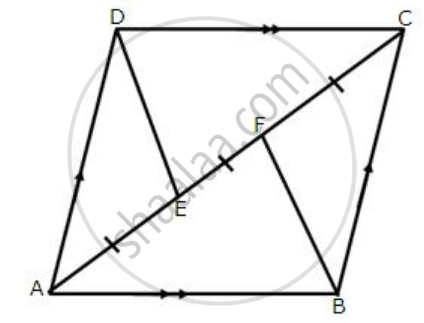
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.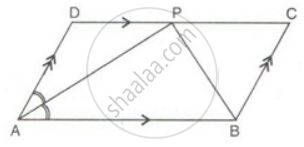
Prove that: BP bisects ∠ABC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.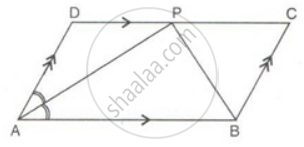
Prove that: ∠APB is a right angle.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD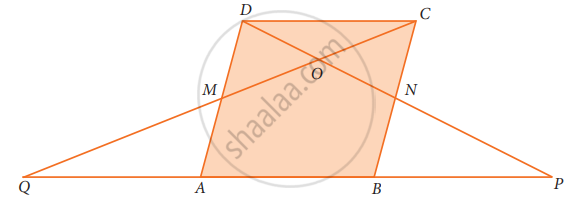
Which of the following statement is correct?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.