Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.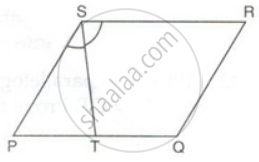
Prove that: RT bisects angle R
उत्तर

Since QT = QR
∠QTR = ∠QRT
But ∠QTR = ∠TRS ...(alternate angles ∵ SR || PQ)
⇒ ∠QRT = ∠TRS
Therefore, RT bisects ∠R.
APPEARS IN
संबंधित प्रश्न
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
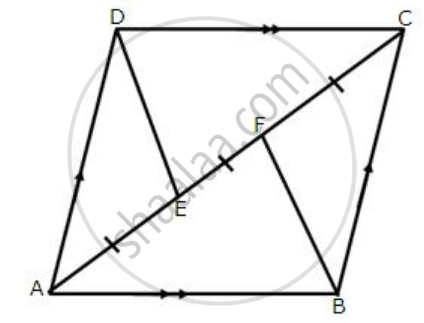
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
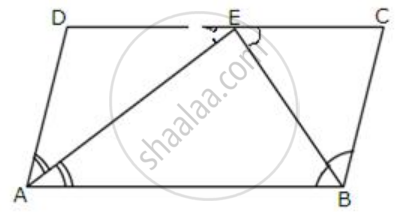
Prove that the bisectors of opposite angles of a parallelogram are parallel.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.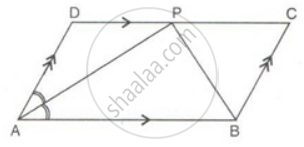
Prove that: ∠APB is a right angle.
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD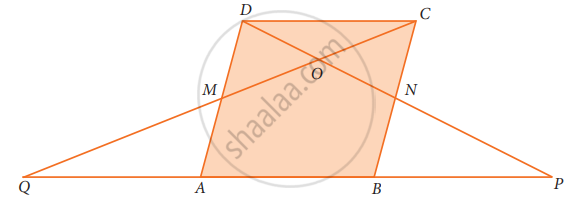
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
